Question

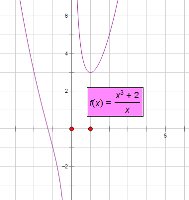
【题目】已知函数的图象与函数的图象有三个不同的交点、、，其中．给出下列四个结论： ①；②；③；④．其中，正确结论的个数有（ ）个

A. 1 B. 2 C. 3 D. 4

Answer 1

【答案】C

【解析】分析：由题意，函数的图象与函数的图象有三个不同的交点，转化为方程有三个不同的实数解，进而函数与的图象有三个不同的交点，利用导数求解函数的单调性和极值，即可得到答案．

详解：由题意，函数的图象与函数的图象有三个不同的交点，

即方程，由三个不同的实数解，即有三个不同的实数解，

即函数与的图象有三个不同的交点，

又由，

当或时，，函数单调递减；

当时，，函数单调递增，

其图象如图所示，且当时，，

要使得函数与的图象有三个不同的交点，则，所以①正确的；

当时，即，解得或，

所以当时，则 所以②是正确的；

结合图象可得，所以③是正确的；

又由，整理得，

又因为，所以，即，

结合③可知，所以④是错误的，故选C．