题目内容
在直角坐标系中，△ABC的两个顶点A，B坐标分别为A（-1，0），B（1，0），平面内两点G、M同时满足下列条件：(1)
+
+
=
，（2）MA=MB=MC，(3)
∥
则△ABC的另一个顶点C的轨迹方程为
| GA |
| GB |
| GC |
| 0 |
| GM |
| AB |
x2+
=1(y≠0)
| y2 |
| 3 |
x2+
=1(y≠0)
．| y2 |
| 3 |
分析：根据MA=MB，可得M在线段AB的中垂线上，从而可得M的坐标，利用
+
+
=
可得重心坐标与C坐标之间的关系，利用MB=MC，即可得到定点C的轨迹方程．
| GA |
| GB |
| GC |
| 0 |
解答：解：（1）设C（x，y），G（x0，y0），M（xm，ym）
∵MA=MB，∴M在线段AB的中垂线上，
∵A（-1，0），B（1，0），∴xm=0
∵
∥
，∴ym=y0…．
∵
+
+
=
，∴（-1-x0，-y0）+（1-x0，-y0）+（x-x0，y-y0）=（0，0）
∴x0=
，y0=
，ym=
∵MB=MC，
∴
=
，
即x2+
=1(y≠0)
∴定点C的轨迹方程为x2+
=1(y≠0)
故答案为：x2+
=1(y≠0)
∵MA=MB，∴M在线段AB的中垂线上，
∵A（-1，0），B（1，0），∴xm=0
∵
| GM |
| AB |
∵
| GA |
| GB |
| GC |
| 0 |
∴x0=
| x |
| 3 |
| y |
| 3 |
| y |
| 3 |
∵MB=MC，
∴
(1-0)2+(0-
|
(x-0)2+(y-
|
即x2+
| y2 |
| 3 |
∴定点C的轨迹方程为x2+
| y2 |
| 3 |
故答案为：x2+
| y2 |
| 3 |
点评：本题考查向量知识的运用，考查曲线的轨迹方程，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
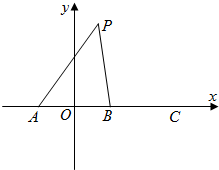如图，在直角坐标系中，A，B，C三点在x轴上，原点O和点B分别是线段AB和AC的中点，已知AO=m（m为常数），平面上的点P满足PA+PB=6m．
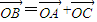（O是坐标原点），其中t∈（0，+∞）．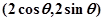
^
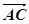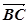,求
的值；