题目内容
如图所示的n×n（n∈N*）的实数数表，满足每一行都是公差为1的等差数列，第一列都是公比为2的等比数列．已知a11=2，则a11+a22+a33+…+ann=分析：首先每一列为等比，可表示出an1，又每一行等差，可表示ann，最后根据通项的特点求和．
解答：解：ann=a11qn-1+（n-1）d=2n+（n-1），所以
a11+a22+…+ann=a11（q1-1+q2-1+…+qn-1）+（1-1）+（2-1）+…（n-1）
=
+
d=2n+1+
-2
故答案为：2n+1+
-2．
a11+a22+…+ann=a11（q1-1+q2-1+…+qn-1）+（1-1）+（2-1）+…（n-1）
=
| a11(qn-1) |
| q-1 |
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
故答案为：2n+1+
| n(n-1) |
| 2 |
点评：主要是找到规律，看横排和竖列．学生要学会从哪些方面找规律，老师要加以引导．
练习册系列答案
相关题目
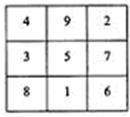（2011•福建模拟）我国的《洛书》中记载着世界上最古老的一个幻方：将1，2，…，9填入3×3的方格内，使三行、三列、二对角线的三个数之和都等于15，如图所示，一般地，将连续的正整数1，2，3，…，n2填入n×n个方格中，使得每行、每列、每条对角线上的数的和相等，这个正方形就叫做n阶幻方，记n阶幻方的对角线上数的和为N，如图1的幻方记为N3=15，那么N12的值为（ ）
如图所示的n×n（n∈N*）的实数数表，满足每一行都是公差为1的等差数列，第一列都是公比为2的等比数列．已知a11=2，则a11+a22+a33+…+ann=________．
我国的《洛书》中记载着世界上最古老的一个幻方：将1，2，…，9填入3×3的方格内，使三行、三列、二对角线的三个数之和都等于15，如图所示，一般地，将连续的正整数1，2，3，…，n2填入n×n个方格中，使得每行、每列、每条对角线上的数的和相等，这个正方形就叫做n阶幻方，记n阶幻方的对角线上数的和为N，如图1的幻方记为N3=15，那么N12的值为