题目内容

我国的《洛书》中记载着世界上最古老的一个幻方：将1，2，…，9填入3×3的方格内，使三行、三列、二对角线的三个数之和都等于15，如图所示，一般地，将连续的正整数1，2，3，…，n²填入n×n个方格中，使得每行、每列、每条对角线上的数的和相等，这个正方形就叫做n阶幻方，记n阶幻方的对角线上数的和为N，如图1的幻方记为N₃=15，那么N₁₂的值为

A.
869
B.
870
C.
875
D.
871

B
分析：根据题意可知，幻方对角线上的数成等差数列，根据等差数列的性质可知对角上的两个数相加正好等于1+n²，进而根据等差数列的求和公式求得答案
解答：根据题意可知，幻方对角线上的数成等差数列，
根据等差数列的性质可知对角上的两个数相加正好等于1+n²，
根据等差数列的求和公式数列的和S= $\text{[math]}$
N₁₂= $\text{[math]}$ =870
故选B．
点评：本题主要考查了等差数列的性质和等差数列的前n项和公式，本题解题的关键是应用等差数列的性质来解题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

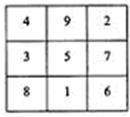（2011•福建模拟）我国的《洛书》中记载着世界上最古老的一个幻方：将1，2，…，9填入3×3的方格内，使三行、三列、二对角线的三个数之和都等于15，如图所示，一般地，将连续的正整数1，2，3，…，n²填入n×n个方格中，使得每行、每列、每条对角线上的数的和相等，这个正方形就叫做n阶幻方，记n阶幻方的对角线上数的和为N，如图1的幻方记为N₃=15，那么N₁₂的值为（　　）

我国的《洛书》中记载着世界上最古老的一个幻方：将1，2，…，9填入3×3的方格内，使三行、三列、二对角线的三个数之和都等于15，如图所示，一般地，将连续的正整数1，2，3，…，n²填入n×n个方格中，使得每行、每列、每条对角线上的数的和相等，这个正方形就叫做n阶幻方，记n阶幻方的对角线上数的和为N，如图1的幻方记为N₃=15，那么N₁₂的值为（）

A．869
B．870
C．875
D．871

我国的《洛书》中记载着世界上最古老的一个幻方：将1，2，…，9填入3×3的方格内，使三行、三列、二对角线的三个数之和都等于15，如图1所示，一般地，将连续的正整数1，2，3，…n²填入n×n个方格中，使得每行、每列、每条对角线上的数的和相等，这个正方形就叫做n阶幻方，记n阶幻方的对角线上数的和为N，如图1的幻方记为N₃=15，那么N₁₂的值为（）

试题分类