Question

【题目】已知函数．

（1）若函数的图象与直线没有交点，求的取值范围；

（2）设，若函数与的图象有且只有一个公共点，求实数的取值范围．

Answer 1

【答案】（1）；（2）或

【解析】

（1）函数没有交点,即方程没有解,可得到方程无解,构造函数,求其值域,进而可求出的取值范围;

（2）两函数只有一个公共点,即方程只有一个解,结合对数的运算性质及二次函数的性质,分类讨论可求出的取值范围.

（1）由题意,方程无解,即方程无解,

令,则函数与的图象无交点.

,

令,因为,所以,

因为函数是上的增函数,所以的值域是,即函数的值域为.

故只需,可使函数与的图象无交点.

即的取值范围是.

（2）由题意,方程只有一个解,

,

即方程为,

则方程只有一个解,

令,则,整理得,该方程有且仅有一个正解.

①当时,则,解得,不符合题意,舍去;

②当时,则为开口向上的二次函数,当时,,

显然,二次函数存在唯一正零点,即方程有且仅有一个正解,符合题意;

③当时,则为开口向下的二次函数.

若一元二次方程有两个相同正解,则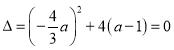,解得或.

时,解得,不合题意,舍去;时,解得,符合题意;

若一元二次方程有两个不同的解,且只有一个正解,则,解得或,且,即,不符合,舍去.

综上,的取值范围是或.