题目内容
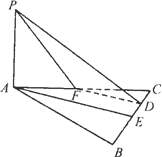
如图,已知PA⊥边长为2的正方形ABCD所在的平面,M,N分别是AB,PC的中点。
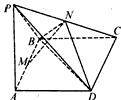
(1)证明:平面DNB⊥平面ABCD;
(2)证明:MN⊥CD;
(3)若直线PB与平面ABCD所成的角为45°,求证:MN⊥平面PCD。
(2)证明:MN⊥CD;
(3)若直线PB与平面ABCD所成的角为45°,求证:MN⊥平面PCD。
|
解:(1)如图,连接AC交BD于O,连接NO, |
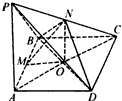 |
| (3)∵直线P与平面ABCD所成的角为45°,且PA⊥平面ABCD ∴∠PBA= 45°,△PAB为等腰直角三角形, ∴PA=AB=AD=2 连接PM,CM,易证△PAM≌△CBM,得PM=CM, ∵N为PC中点, ∴MN⊥PC 又MN⊥CD,PC∩CD=C ∴MN⊥平面PCD。 |

练习册系列答案
相关题目
 平面DNB,
平面DNB,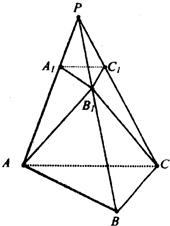 (2008•河西区三模)如图,已知三棱锥P-ABC,A1,B1,C1分别在棱PA、PB、PC上,且面A1B1C1∥面ABC,又面AB1C⊥面ABC.△AB1C为边长是4的等边三角形,∠ACB=90°,BC=2.
(2008•河西区三模)如图,已知三棱锥P-ABC,A1,B1,C1分别在棱PA、PB、PC上,且面A1B1C1∥面ABC,又面AB1C⊥面ABC.△AB1C为边长是4的等边三角形,∠ACB=90°,BC=2.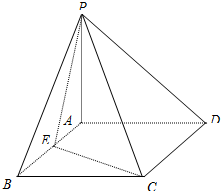 (2007•肇庆二模)如图,已知四棱锥P-ABCD,底面是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,E为AB的中点.
(2007•肇庆二模)如图,已知四棱锥P-ABCD,底面是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,E为AB的中点.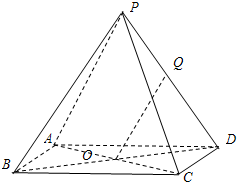 (2007•静安区一模)(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.
(2007•静安区一模)(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.