题目内容
如图,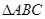 在平面
在平面 内,
内, ,
, ,P为平面
,P为平面 外一个动点,且PC=
外一个动点,且PC= ,
,

(1)问当PA的长为多少时,
(2)当 的面积取得最大值时,求直线BC与平面PAB所成角的大小
的面积取得最大值时,求直线BC与平面PAB所成角的大小
(1) ;(2)
;(2)
解析试题分析:(1)由分析可知当 时,
时, ,则
,则 ,由勾股定理可求得
,由勾股定理可求得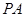 。(2)因为
。(2)因为 为定值,且
为定值,且 ,
, ,所以当
,所以当 时,
时, 的面积取得最大值。分析可知
的面积取得最大值。分析可知 均是以
均是以 为底的等腰三角形,故取
为底的等腰三角形,故取 中点
中点 ,连接
,连接 。则有
。则有 ,从而可得
,从而可得 ,可知
,可知 就是直线
就是直线 与平面PAB所成角,在
与平面PAB所成角,在 中可求此角。
中可求此角。
试题解析:(1)因为 ,所以
,所以 ,当
,当 时,
时, ,而
,而 ,所以
,所以 ,此时,
,此时, ,即当PA=
,即当PA= 时,
时,
(2)
在 中,因为PC=
中,因为PC= ,
, ,
, ,所以
,所以 ,当
,当 的面积取得最大值时,
的面积取得最大值时, ,(如图)在
,(如图)在 中,因为
中,因为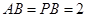 ,取
,取 中点
中点 ,连接
,连接 。则
。则 ,因为
,因为 且点
且点 为
为 中点,所以
中点,所以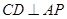 ,因为
,因为 ,所以
,所以 ,由此可求得
,由此可求得 ,又在
,又在 中,
中, ,所以
,所以 ,由于
,由于 ,所以
,所以 ,所以
,所以 就是直线
就是直线 与平面PAB所成角,在
与平面PAB所成角,在 中,因为
中,因为 ,所以
,所以 ,所以直线BC与平面
,所以直线BC与平面 所成角的大小为
所成角的大小为
考点:1线线垂直、线面垂直;2线面角。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,D是AC的中点.
,D是AC的中点.
 是母线
是母线 的中点,
的中点, 是底面圆的直径,底面半径
是底面圆的直径,底面半径 与母线
与母线 所成的角的大小等于
所成的角的大小等于 .
.
 时,求异面直线
时,求异面直线 与
与 所成的角;
所成的角; 的体积最大时,求
的体积最大时,求 底面ABCD,
底面ABCD, ,E是PA的中点.
,E是PA的中点.
 平面EBD;
平面EBD;
 ?,若存在,求出AM的长,若不存在,说明理由
?,若存在,求出AM的长,若不存在,说明理由 中,侧面
中,侧面 ⊥底面
⊥底面 ,侧棱
,侧棱 与底面
与底面 .底面
.底面 点,
点, 是线段
是线段 上一点,且
上一点,且 .
.
 //侧面
//侧面 与底面
与底面 关于直线
关于直线 对称,
对称,
 .把
.把 沿
沿 折起(如图二),使二面角
折起(如图二),使二面角 的余弦值等于
的余弦值等于 .对于图二,完成以下各小题:
.对于图二,完成以下各小题:
 两点间的距离;
两点间的距离; 平面
平面 ;
; 所成角的正弦值.
所成角的正弦值. 中,
中, ,
, ,求:
,求:
 与
与 所成角的余弦值;
所成角的余弦值;  的距离.
的距离.