题目内容
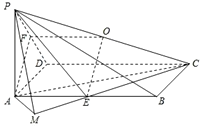
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点,
(1)证明:PF⊥FD;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值。
(1)证明:PF⊥FD;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值。

|
解:(Ⅰ)∵ |
 |

练习册系列答案
相关题目
 平面
平面 ,
, ,AB=1,AD=2,
,AB=1,AD=2, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,得
,得 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, 的点G即为所求。
的点G即为所求。 是平面PAD的法向量,易得
是平面PAD的法向量,易得 ,
, 是PB与平面ABCD所成的角,
是PB与平面ABCD所成的角, ,PA=1,
,PA=1, ,
, ,
, 。
。 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点. (2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点.
(2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点. (2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点.
(2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点. 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ< (2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.