题目内容
已知点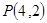 是直线
是直线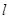 被椭圆
被椭圆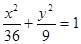 所截得的线段中点,求直线
所截得的线段中点,求直线 的方程。
的方程。
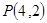 是直线
是直线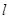 被椭圆
被椭圆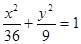 所截得的线段中点,求直线
所截得的线段中点,求直线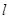 的方程。
的方程。
试题分析:由题意可设
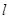 的方程为:
的方程为: 即
即
由

整理,得


又

 的中点为
的中点为

解得

将
 代入
代入 ,得
,得 ,经验证
,经验证
所以
 满足题目要求
满足题目要求 所求
所求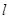 的方程为:
的方程为: 即
即
点评:直线与椭圆相交的中点弦问题的求解一般有两种思路:其一,设出直线方程,与椭圆方程联立将中点坐标转化为两交点坐标,其二,采用点差法,即将两交点坐标分别代入椭圆方程,得到的两式子相减即可得到直线斜率,两种方法都要验证所求直线是否满足与椭圆有两交点

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
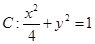 的上、下顶点分别为
的上、下顶点分别为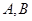 ,点
,点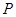 在椭圆上,且异于点
在椭圆上,且异于点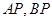 与直线
与直线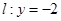 分别交于点
分别交于点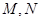 ,
,
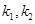 ,求证:
,求证: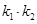 为定值;
为定值; 的长的最小值;
的长的最小值;



 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. 的离心率为 ( )
的离心率为 ( )



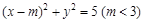 与椭圆E:
与椭圆E: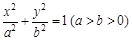 有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
 的取值范围.
的取值范围.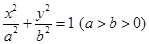 过点
过点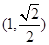 ,离心率为
,离心率为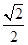 ,左、右焦点分别为
,左、右焦点分别为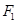 、
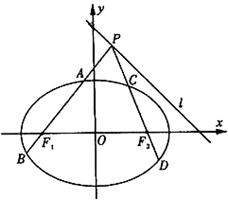
、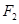 .点
.点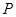 为直线
为直线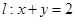 上且不在
上且不在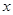 轴上的任意一点,直线
轴上的任意一点,直线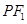 和
和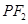 与椭圆的交点分别为
与椭圆的交点分别为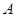 、
、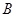 和
和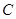 、
、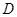 ,
,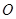 为坐标原点.设直线
为坐标原点.设直线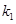 、
、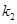 .
.
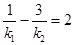 ;
;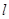 上是否存在点
上是否存在点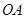 、
、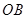 、
、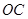 、
、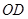 的斜率
的斜率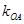 、
、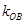 、
、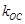 、
、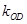 满足
满足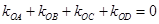 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点 (a>b>0),则称以原点为圆心,r=
(a>b>0),则称以原点为圆心,r= 的圆为椭圆C的“知己圆”。
的圆为椭圆C的“知己圆”。 ;求椭圆C方程及其“知己圆”的方程;
;求椭圆C方程及其“知己圆”的方程;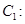
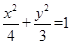 ,其左准线为
,其左准线为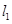 ,右准线为
,右准线为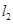 ,抛物线
,抛物线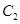 以坐标原点
以坐标原点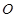 为顶点,
为顶点, 两点.
两点. 的长度.
的长度.