题目内容
18．若方程${（\frac{1}{4}）^x}+{（\frac{1}{2}）^{x-1}}$-a=0有正数解，则实数a的取值范围是（ ）| A． | 0＜a＜1 | B． | -3＜a＜0 | C． | 0＜a＜3 | D． | -1＜a＜0 |
分析 为便于处理，不妨设t=$（\frac{1}{2}）^{x}$，于是可转化为求关于t的方程t2+2t-a=0的根的问题，明显地，原方程有正实数解，即可转化为关于t的方程在（0，1）上有解的问题．于是问题迎刃而解．
解答 解：设t=$（\frac{1}{2}）^{x}$，则有：a=t2+2t=（t+1）2-1．
原方程有正数解x＞0，则0＜t＜1，
即关于t的方程t2+2t-a=0在（0，1）上有实根．
又因为a=（t+1）2-1．
所以当0＜t＜1时有1＜t+1＜2，
即1＜（t+1）2＜4，
即0＜（t+1）2-1＜3，
即得0＜a＜3．
故选：C．
点评 本题考查函数最值的求法，二次方程根的分布问题，以及对含参数的函数、方程的问题的考查，亦对转化思想，换元法在解题中的应用进行了考查．
练习册系列答案
相关题目
8．
一个空间几何体的三视图如图，其中正视图是边长为2的正三角形，俯视图是边长分别为1，2的矩形，则该几何体的侧面积为（ ）
一个空间几何体的三视图如图，其中正视图是边长为2的正三角形，俯视图是边长分别为1，2的矩形，则该几何体的侧面积为（ ）| A． | $\sqrt{3}$+4 | B． | $\sqrt{3}$+6 | C． | 2$\sqrt{3}$+4 | D． | 2$\sqrt{3}$+6 |
6．已知椭圆E：$\frac{x^2}{4}+\frac{y^2}{2}=1$，直线l交椭圆于A，B两点，若AB的中点坐标为（$\frac{1}{2}$，-1），则l的方程为（ ）
| A． | 2x+y=0 | B． | $x-2y-\frac{5}{2}=0$ | C． | 2x-y-2=0 | D． | $x-4y-\frac{9}{2}=0$ |
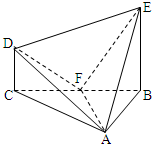在几何体ABCDE中，∠BAC=$\frac{π}{2}$，DC⊥平面ABC，EB⊥平面ABC，AB=AC=BE=2，CD=1，设F是BC的中点．
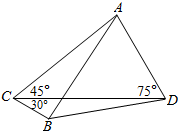在一次抗雪救灾中，需要在A、B两地之间架设高压电线，为测量A、B两地的距离，救援人员在相距l米的C、D两地（A，B，C，D在同一平面上），测得∠ACD=45°，∠BCD=30°∠ADC=75°（如图），考虑到电线在自然下垂和施工损耗等原因，实际所得电线长度大于应是A、B距离的1.2倍，问救援至少英爱准备多长的电线？