题目内容
如图,在△ABC中,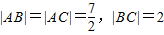 ,以B、C为焦点的椭圆恰好过AC的中点P.
,以B、C为焦点的椭圆恰好过AC的中点P.(1)求椭圆的标准方程;
(2)过椭圆的右顶点A1作直线l与圆E:(x-1)2+y2=2相交于M、N两点,试探究点M、N能将圆E分割成弧长比值为1:3的两段弧吗?若能,求出直线l的方程;若不能,请说明理由.
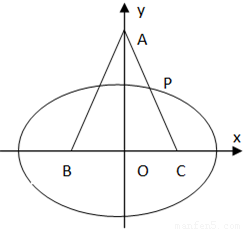
【答案】分析:(1)确定A,C的坐标,即可得到P的坐标,利用椭圆的定义,求得长轴长,进而可求椭圆的方程;
(2)椭圆的右顶点A1(2,0),圆E的圆心为E(1,0),半径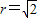 ,假设点M、N能将圆E分割成弧长比值为1:3的两段弧,则可得∠MEN=90°,圆心E(1,0)到直线l的距离,分类讨论:当直线l斜率不存在时,l的方程为x=2;当直线l斜率存在时,设l的方程为y=k(x-2),即kx-y-2k=0,求出圆心E(1,0)到直线l的距离即可得到结论.
,假设点M、N能将圆E分割成弧长比值为1:3的两段弧,则可得∠MEN=90°,圆心E(1,0)到直线l的距离,分类讨论:当直线l斜率不存在时,l的方程为x=2;当直线l斜率存在时,设l的方程为y=k(x-2),即kx-y-2k=0,求出圆心E(1,0)到直线l的距离即可得到结论.
解答: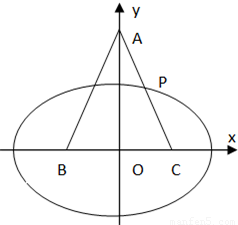 解:(1)∵
解:(1)∵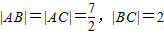
∴|BO|=|OC|=1,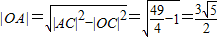 …(2分)
…(2分)
∴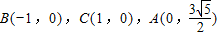
∴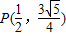 …(4分)
…(4分)
依椭圆的定义有: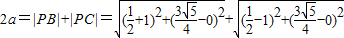 =
=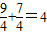
∴a=2,…(6分)
又c=1,∴b2=a2-c2=3…(7分)
∴椭圆的标准方程为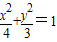 …(8分)
…(8分)
(2)椭圆的右顶点A1(2,0),圆E的圆心为E(1,0),半径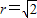 .
.
假设点M、N能将圆E分割成弧长比值为1:3的两段弧,则∠MEN=90°,圆心E(1,0)到直线l的距离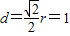 …(10分)
…(10分)
当直线l斜率不存在时,l的方程为x=2,此时圆心E(1,0)到直线l的距离d=1(符合)…(11分)
当直线l斜率存在时,设l的方程为y=k(x-2),即kx-y-2k=0,
∴圆心E(1,0)到直线l的距离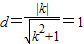 ,无解…(13分)
,无解…(13分)
综上:点M、N能将圆E分割成弧长比值为1:3的两段弧,此时l方程为x=2…(14分).
点评:本题考查椭圆的标准方程,考查椭圆的定义,考查直线与圆的位置关系,属于中档题.
(2)椭圆的右顶点A1(2,0),圆E的圆心为E(1,0),半径
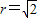 ,假设点M、N能将圆E分割成弧长比值为1:3的两段弧,则可得∠MEN=90°,圆心E(1,0)到直线l的距离,分类讨论:当直线l斜率不存在时,l的方程为x=2;当直线l斜率存在时,设l的方程为y=k(x-2),即kx-y-2k=0,求出圆心E(1,0)到直线l的距离即可得到结论.
,假设点M、N能将圆E分割成弧长比值为1:3的两段弧,则可得∠MEN=90°,圆心E(1,0)到直线l的距离,分类讨论:当直线l斜率不存在时,l的方程为x=2;当直线l斜率存在时,设l的方程为y=k(x-2),即kx-y-2k=0,求出圆心E(1,0)到直线l的距离即可得到结论.解答:
 解:(1)∵
解:(1)∵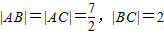
∴|BO|=|OC|=1,
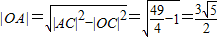 …(2分)
…(2分)∴
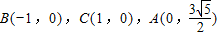
∴
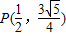 …(4分)
…(4分)依椭圆的定义有:
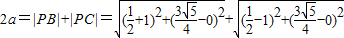 =
=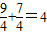
∴a=2,…(6分)
又c=1,∴b2=a2-c2=3…(7分)
∴椭圆的标准方程为
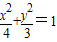 …(8分)
…(8分)(2)椭圆的右顶点A1(2,0),圆E的圆心为E(1,0),半径
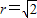 .
.假设点M、N能将圆E分割成弧长比值为1:3的两段弧,则∠MEN=90°,圆心E(1,0)到直线l的距离
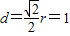 …(10分)
…(10分)当直线l斜率不存在时,l的方程为x=2,此时圆心E(1,0)到直线l的距离d=1(符合)…(11分)
当直线l斜率存在时,设l的方程为y=k(x-2),即kx-y-2k=0,
∴圆心E(1,0)到直线l的距离
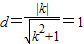 ,无解…(13分)
,无解…(13分)综上:点M、N能将圆E分割成弧长比值为1:3的两段弧,此时l方程为x=2…(14分).
点评:本题考查椭圆的标准方程,考查椭圆的定义,考查直线与圆的位置关系,属于中档题.

练习册系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知