题目内容
求半径为1,且与圆x2+y2=4相切的动圆圆心的轨迹方程.
答案:
解析:
提示:
解析:
|
解:设动圆圆心为M.若两圆内切,则|MO|=|2-1|=1,由圆的定义M点轨迹是以O为圆心,1为半径的圆,圆的方程为x2+y2=1;若两圆外切,则|MO|=|2+1|=3,由圆的定义M点轨迹是以O为圆心,3为半径的圆,方程为x2+y2=9.这两种情况也可合并为(x2+y2-1)·(x2+y2-9)=0. |
提示:
|
动圆与圆x2+y2=4可能外切,也可能内切,所以应分情况讨论. |

练习册系列答案
相关题目
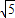 ,且与直线x+2y-6=0切于点P(2,2).
,且与直线x+2y-6=0切于点P(2,2).