题目内容
下列不等式对任意的
恒成立的是（ ）
A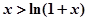． | B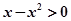． | C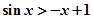． | D． |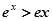
A
解析试题分析：当x=1时，ex=ex，故A中ex＞ex对任意的x∈（0，+∞）不恒成立；当x=1时，x-x2=0，故B中x-x2＞0对任意的x∈（0，+∞）不恒成立；又∵y=sin在（0，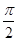
）上函数值由0递增到1，y=-x+1在（0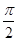，）上函数值由1递减到1-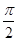，故在区间（0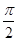，）上存在实数x使sinx=-x+1，故C中sinx＞-x+1对任意的x∈（0，+∞）不恒成立；而∵函数y=x-ln（1+x）的导函数y'=1-
在x∈（0，+∞）有，y'＞0恒成立,故y=x-ln（1+x）在区间（0，+∞）上为增函数，y＞y|x=0=0，故x＞ln（1+x）对任意的x∈（0，+∞）恒成立，故选D．
考点：不等式恒成立问题
练习册系列答案
相关题目
设
，
，
，（e是自然对数的底数），则
A． | B． | C． | D． |
已知
且
，则“
”是“
”的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
设
是定义在
上的函数，若
，且对任意
，满足
，
，则
=（ ）
A． | B． | C． | D． |
若
，则下列不等式成立的是( )
A． | B． |
C． | D． |
设
，则下列不等式成立的是( )
A． | B． | C． | D． |
已知m>1，a＝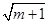
－
，b＝－
，则以下结论正确的是( )
| A．a>b | B．a＝b |
| C．a<b | D．a，b的大小不确定 |
不等式
恒成立,则实数a的取范围是( )
A． |
B． |
C． |
D． |
函数f（x）=
的定义域为（ ）
| A．（﹣3，0] |
| B．（﹣3，1] |
| C．（﹣∞，﹣3）∪（﹣3.0） |
| D．（﹣∞，﹣3）∪（﹣3，1） |