题目内容
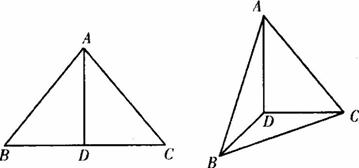
将边长为2的正△ABC沿高AD折成直二面角B-AD-C，则三棱锥B-ACD的外接球的表面积为 ( )A.5π B.
π C.10π D.20π
答案：A 【解析】本题考查图形的折叠、二面角的平面角以及球的内接长方体的性质等知识.如图所示,在正三角形ABC中AD⊥BC,所以可得折叠图形中,有AD⊥DC,AD⊥DB,则∠BDC为直二面角B-AD-C的平面角.所以∠BDC=90°.由于三棱锥B-ACD内接于球,所以以AD、BD、CD为三条棱补成一个长方体,则这个长方体也内接于此球.那么球的直径就是长方体的体对角线.于是有2R=l=
,则球的半径r=
,所以S球=4πR2=5π.
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
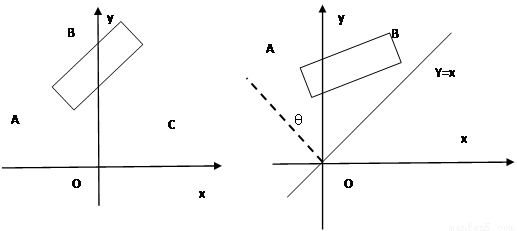
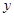轴的正半轴上，O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.
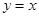的交点为N.设
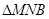的周长为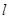
,在正方形OABC旋转的过程中
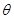，当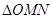
的面积最小？求出这个最小值， 并求出此时△BMN的内切圆半径.
，CD是AB边上的高，E、F分别是AC和BC边的中点．现将△ABC沿CD翻折成直二面角A―DC―B，如图b所示．
