题目内容
【题目】已知函数![]() ,其中e是自然对数的底数,
,其中e是自然对数的底数,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)设![]() ,讨论函数
,讨论函数![]() 零点的个数,并说明理由.
零点的个数,并说明理由.
【答案】(1)增区间是![]() ,减区间是
,减区间是![]() .(2)见解析
.(2)见解析
【解析】
(1)求导函数![]() ,分别令
,分别令![]() ,解出不等式,即可得到函数
,解出不等式,即可得到函数![]() 的单调区间;
的单调区间;
(2)由![]() 得方程
得方程 ![]() ,显然
,显然 ![]() 为此方程的一个实数解.当
为此方程的一个实数解.当![]() 时, 方程可化简为
时, 方程可化简为![]() ,设函数
,设函数![]() 利用导数得到
利用导数得到 ![]() 的最小值, 因为
的最小值, 因为![]() ,再对
,再对![]() 讨论,得到函数
讨论,得到函数![]() 的零点个数.
的零点个数.
解:(1)因为![]() ,所以
,所以![]() .
.
由![]() 得
得![]() ;由
;由![]() 得
得![]() .
.
所以由![]() 的增区间是
的增区间是![]() ,减区间是
,减区间是![]() .
.
(2)因为![]() .
.
由![]() ,得
,得![]() 或
或![]() .
.
设![]() ,又
,又![]() 即
即![]() 不是
不是![]() 的零点,
的零点,
故只需再讨论函数![]() 零点的个数.
零点的个数.
因为![]() ,
,
所以当![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增.
单调递增.
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
①当![]() 即
即![]() 时,无零点;
时,无零点;
②当![]() 即
即![]() 时,
时, ![]() 有唯一零点;
有唯一零点;
③当![]() ,即
,即![]() 时,因为
时,因为![]() ,
,
所以![]() 在
在![]() 上有且只有一个零点.
上有且只有一个零点.
令![]() 则
则![]() .
.
设![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以,![]() 都有
都有![]() .
.
所以![]() .
.
所以![]() 在
在![]() 上有且只有一个零点.
上有且只有一个零点.
所以当![]() 时,
时,![]() 有两个零点
有两个零点
综上所述,当![]() 时,
时,![]() 有一个零点;
有一个零点;
当![]() 时,
时,![]() 有两个零点;
有两个零点;
当![]() 时,
时,![]() 有三个零点.
有三个零点.

练习册系列答案
相关题目
【题目】已知x与y之间的几组数据如表:
x | 1 | 2 | 3 | 4 |
y | 1 | m | n | 4 |
如表数据中y的平均值为2.5,若某同学对m赋了三个值分别为1.5,2,2.5,得到三条线性回归直线方程分别为![]() ,
,![]() ,
,![]() ,对应的相关系数分别为
,对应的相关系数分别为![]() ,
,![]() ,
,![]() ,下列结论中错误的是( )
,下列结论中错误的是( )
参考公式:线性回归方程![]() 中,其中
中,其中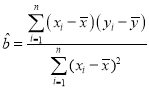 ,
,![]() .相关系数
.相关系数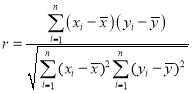 .
.
A.三条回归直线有共同交点B.相关系数中,![]() 最大
最大
C.![]() D.
D.![]()