Question

【题目】已知直线与轴，轴分别交于，，线段的中垂线与抛物线有两个不同的交点、．

（1）求的取值范围；

（2）是否存在，使得，，，四点共圆，若存在，请求出的值，若不存在，请说明理由．

Answer 1

【答案】（1）（2）存在，

【解析】

（1）求出两点坐标，得出其中垂线方程为，与抛物线方程联立根据即可得结果；

（2）设，，线段的中点为，将（1）和韦达定理可得，，结合四点共圆的特征得，代入两点间距离公式可解得的值.

（1）因为直线与轴，轴分别交于，.

所以，，

所以线段的中点为，，

所以线段的中垂线的方程为，即.

将代入，

得，

因为与有两个不同的交点，.

所以，

又，所以，即的取值范围为.

（2）若，，，四点共圆，由对称性可知，圆心应为线段的中点，

设，，线段的中点为，

则，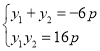

所以，，

若，，C，四点共圆，则，即，

所以.

所以，解得，

又满足，所以存在，使得，，C，四点共圆.