题目内容
已知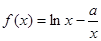 (
(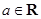 ).
).
(Ⅰ)当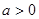 时,判断
时,判断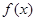 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)若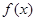 在
在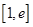 上的最小值为
上的最小值为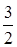 ,求
,求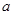 的值;
的值;
(Ⅲ)若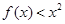 在
在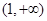 上恒成立,试求
上恒成立,试求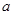 的取值范围.
的取值范围.
【答案】
(1)单调递增;(2)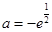 ;(3)
;(3)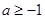 .
.
【解析】
试题分析:(1)判断函数的单调性常用作差比较法、导函数法.其共同点都是与0比大小确定单调性.也可以利用基本初等函数的单调性来判断:当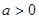 时,因为
时,因为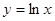 与
与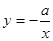 在
在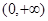 上都是单调递增,所以
上都是单调递增,所以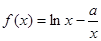 (
(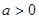 )在定义域
)在定义域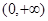 上单调递增;(2)利用导函数法求闭区间上的最值,首先要求出极值,然后再与两个端点函数值比较得出最值;既要灵活利用单调性,又要注意对字母系数
上单调递增;(2)利用导函数法求闭区间上的最值,首先要求出极值,然后再与两个端点函数值比较得出最值;既要灵活利用单调性,又要注意对字母系数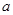 进行讨论;(3)解决“恒成立”问题,常用分离参数法,转化为求新构造函数的最值(或值域).
进行讨论;(3)解决“恒成立”问题,常用分离参数法,转化为求新构造函数的最值(或值域).
试题解析:(1)由题意得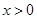 ,且
,且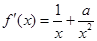 1分
1分
显然,当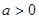 时,
时,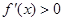 恒成立,
恒成立,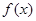 在定义域上单调递增;
3分
在定义域上单调递增;
3分
(2)当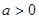 时由(1)得
时由(1)得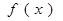 在定义域上单调递增,
在定义域上单调递增,
所以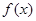 在
在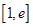 上的最小值为
上的最小值为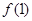 , 4分
, 4分
即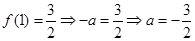 (与
(与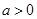 矛盾,舍);
5分
矛盾,舍);
5分
当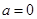 ,
,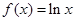 显然在
显然在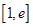 上单调递增,最小值为0,不合题意;
6分
上单调递增,最小值为0,不合题意;
6分
当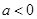 ,
,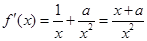 ,
,
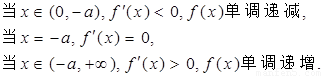 7分
7分
若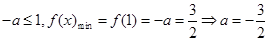 (舍);
(舍);
若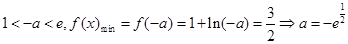 (满足题意);
(满足题意);
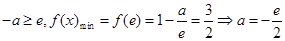 (舍); 8分
(舍); 8分
综上所述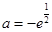 .
9分
.
9分
(3)若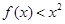 在
在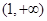 上恒成立,即在
上恒成立,即在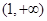 上
上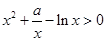 恒成立,(分离参数求解)
恒成立,(分离参数求解)
等价于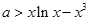 在
在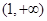 恒成立,令
恒成立,令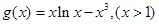 .
.
则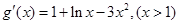 ;
10分
;
10分
令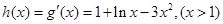 ,则
,则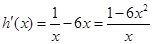
显然当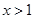 时
时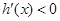 ,
,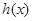 在
在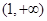 上单调递减,
上单调递减,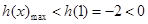 ,
,
即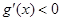 恒成立,说明
恒成立,说明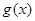 在
在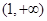 单调递减,
单调递减,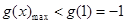 ; 11分
; 11分
所以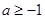 . 12分
. 12分
考点:函数的单调性、导数及其应用

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力.每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%.假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(Ⅰ)任选1名下岗人员,求该人参加过培训的概率;
(Ⅱ)任选3名下岗人员,记ξ为3人中参加过培训的人数,求ξ的分布列和期望.
(Ⅰ)任选1名下岗人员,求该人参加过培训的概率;
(Ⅱ)任选3名下岗人员,记ξ为3人中参加过培训的人数,求ξ的分布列和期望.
| ξ | 0 | 1 | 2 | 3 |
| P | 0.021 | 0.027 | 0.243 | 0.729 |
已知函数f(x)=-x3+ax2-x-1在(-∞,+∞)上是单调函数,则实数a的取值范围是( )
A、(-∞,-
| ||||
B、[-
| ||||
C、(-∞,-
| ||||
D、(-
|
已知函数f(x)=
若f(2-a2)>f(a),则实数a的取值范围是( )
|
| A、(-∞,-1)∪(2,+∞) |
| B、(-1,2) |
| C、(-2,1) |
| D、(-∞,-2)∪(1,+∞) |