题目内容
已知数列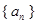 是首项为
是首项为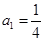 ,公比
,公比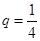 的等比数列. 设
的等比数列. 设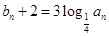
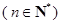 ,数列
,数列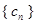 满足
满足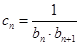 .
.
(Ⅰ)求证:数列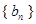 成等差数列;
成等差数列;
(Ⅱ)求数列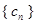 的前
的前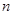 项和
项和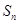 .
.
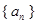 是首项为
是首项为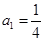 ,公比
,公比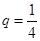 的等比数列. 设
的等比数列. 设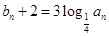
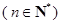 ,数列
,数列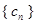 满足
满足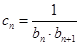 .
.(Ⅰ)求证:数列
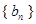 成等差数列;
成等差数列; (Ⅱ)求数列
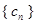 的前
的前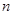 项和
项和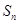 .
. (1)根据数列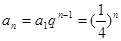 ,然后结合
,然后结合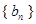 与
与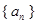 的关系式化简得到
的关系式化简得到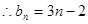 ,加以证明。
,加以证明。
(2)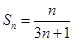
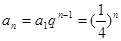 ,然后结合
,然后结合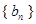 与
与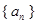 的关系式化简得到
的关系式化简得到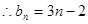 ,加以证明。
,加以证明。(2)
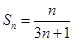
试题分析:解:(Ⅰ)由已知可得,
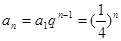 ,
,
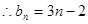
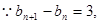
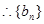 为等差数列,其中
为等差数列,其中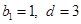 . 6分
. 6分 (Ⅱ)
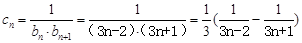 ,
, 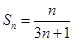 12分
12分点评:解决的关键是能结合数列的定义来证明等差数列或者等比数列,同时能结合裂项法思想求和,属于基础题。

练习册系列答案
相关题目

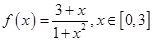 ,已知数列
,已知数列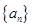 满足
满足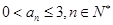 ,且
,且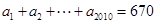 ,则
,则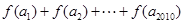 ( )
( ) 中,若
中,若 ,则
,则 = 。
= 。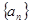 ,定义
,定义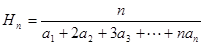 ,若
,若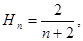 则数列
则数列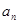 的通项公式为 。
的通项公式为 。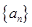 、
、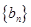 的前
的前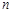 项和分别为
项和分别为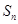 、
、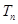 ,对任意的
,对任意的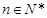 都
都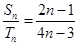 ,则
,则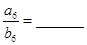
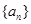 的前
的前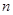 项和为
项和为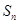 ,点
,点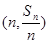 在直线
在直线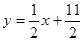 上.数列
上.数列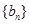 满足
满足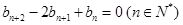 ,且
,且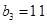 ,前9项和为153.
,前9项和为153.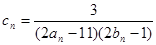 ,数列
,数列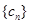 的前
的前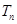 ,求使不等式
,求使不等式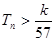 对一切
对一切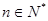 都成立的最大正整数
都成立的最大正整数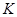 的值;
的值;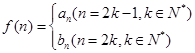 ,问是否存在
,问是否存在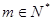 ,使得
,使得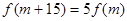 成立?若存在,求出
成立?若存在,求出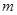 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 
 满足
满足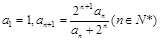 .
.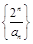 是等差数列;
是等差数列;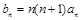 ,求数列
,求数列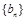 的前
的前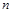 项和
项和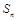 .
.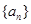 为等比数列,
为等比数列,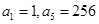 ;
;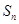 为等差数列
为等差数列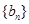 的前n项和,
的前n项和,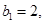
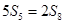 .
.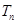
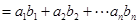 ,求
,求