题目内容
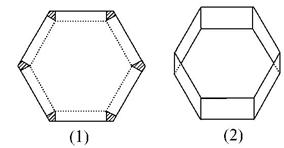
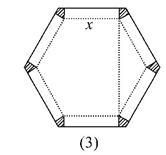
如图(1)所示,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器,如图(2)所示,求这个正六棱柱容器容积的最大值.


【解题指南】设出变量表示出容器的容积,利用三个正数的平均不等式求解.
解:设正六棱柱容器底面边长为x(x>0),高为h,
由图(3)可有2h+
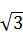 x=
x=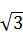 ,
,所以h=
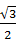 (1-x),V=S底·h=6×
(1-x),V=S底·h=6×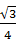 x2·h=
x2·h=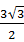 x2·
x2·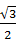 ·(1-x)=2
·(1-x)=2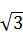 ×
×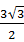 ×
× ×
× ×(1-x)
×(1-x)≤9×
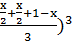 =
= .
.当且仅当
 =1-x,即x=
=1-x,即x= 时,等号成立.
时,等号成立.所以当底面边长为
 时,正六棱柱容器容积最大,为
时,正六棱柱容器容积最大,为 .
.
练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 +
+ =1,x+y的最小值为18,求a,b.
=1,x+y的最小值为18,求a,b. 、
、 ,若
,若 ,则下列不等式中正确的是( )
,则下列不等式中正确的是( )


