Question

已知tanα=3，求下列两个式子的值.

(1)；

(2)2sin²α+sinαcosα-3cos²α.

Answer 1

思路解析：(1)为了直接利用tanα=3，注意所求值式的分子、分母均为一次齐次式(sinα、cosα的次数相同)，把分子、分母同除以cosα(cosα≠0)，将分子、分母转化为tanα为元的代数式.也可利用平方关系sin²α+cos²α=1将分子、分母都变为二次齐次式，再利用商数关系式归为关于tanα的分式求值.

解：(1).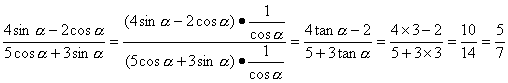

(2)解法一：∵tanα=3,

又cos²α==,

∴原式=2cos²αtan²α+cos²αtanα-3cos²α

=cos²α(2tan²α+tanα-3)

=(2×3²+3-3)

=.

解法二：原式=

.