题目内容
已知△ABC中，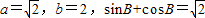
，则角A=（ ）A．30°
B．45°
C．90°
D．150°
【答案】分析：先利用辅助角公式求出角B，然后利用正弦定理求出角A即可，注意三角形的内角和为180°．
解答：解：∵sinB+cosB=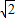
∴
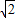sin（B+45°）=
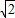解得sin（B+45°）=1
∴B=45°或135°则sinB=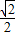
根据正弦定理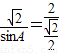
解得sinA=
解得A=30°或150°（舍去）
故选A．
点评：本题主要考查了辅助角公式，以及正弦定理的应用，同时考查了运算求解的能力，属于基础题．
解答：解：∵sinB+cosB=
∴
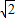
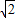sin（B+45°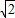）=解得sin（B+45°）=1∴B=45°或135°则sinB=
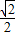
根据正弦定理
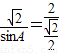
解得sinA=
解得A=30°或150°（舍去）故选A．
点评：本题主要考查了辅助角公式，以及正弦定理的应用，同时考查了运算求解的能力，属于基础题．
练习册系列答案
综合自测系列答案
相关题目
的取值范围是( )
］ C.(1,
］ D.［1,
］
，则
(B) 
(C) 
(D) 
，则
B. 
C. 
D. 
，则
_______________.