题目内容
已知函数
。
（1）若函数在区间
上存在极值，其中
，求实数
的取值范围；
（2）如果当
时，不等式
恒成立，求实数
的取值范围；
（3）求证：
解：（1）因为
当
当
所以
上单调递增；在
上单调递减，所以
函数
处取得极大值。因为函数
，解得
。…………4分
（2）不等式
记
所以
，令
=
1>0
从而
上也单调递增，所以
。
………………………………………………………………9分
（3）由（2）知：当
，
，
令
则
所以
，…，叠加得：
=
。
则
所以………………14分
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
．
，试确定函数
的单调区间；（2）若
，且对于任意
，
恒成立，试确定实数
的取值范围；（3）设函数
，求证：
．
，
，求
的单调区间；
时，求证：
．
．
为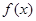
的极值点，求实数
的值；
在
上为增函数，求实数
时，方程
有实根，求实数
的最大值．
。
，求函数
的值；
．
中任取一个元素
，从集合
中任取一个元素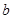
，求方程
有两个不相等实根的概率；
中任取的一个数，
中任取的一个数，求方程