题目内容
等差数列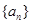 的各项均为正数,
的各项均为正数,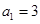 ,前
,前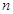 项和为
项和为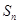 ,
,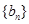 为等比数列,
为等比数列, 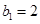 ,且
,且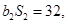
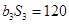 .
.
(1)求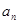 与
与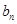 ;
;
(2)求数列 的前
的前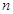 项和
项和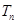 .
.
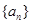 的各项均为正数,
的各项均为正数,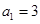 ,前
,前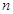 项和为
项和为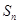 ,
,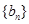 为等比数列,
为等比数列, 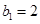 ,且
,且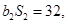
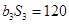 .
.(1)求
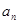 与
与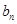 ;
;(2)求数列
 的前
的前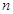 项和
项和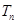 .
.(1) ;(2)
;(2)
 ;(2)
;(2)
试题分析:
 (1)
(1) 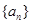 的公差为
的公差为 ,
,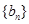 的公比为
的公比为 ,利用等比数列的通项公式和等差数列的前
,利用等比数列的通项公式和等差数列的前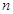 项和公式,由
项和公式,由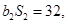
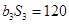 列出关于
列出关于 的方程组,解出
的方程组,解出 的值,从而得到
的值,从而得到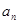 与
与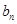 的表达式.
的表达式.(2)根据数列
 的特点,可用错位相减法求它的前
的特点,可用错位相减法求它的前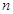 项和
项和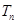 ,由(1)的结果知
,由(1)的结果知
 ,两边同乘以2得
,两边同乘以2得
由(1)(2)两式两边分别相减,可转化为等比数列的求和问题解决.
试题解析:(1)设
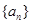 的公差为
的公差为 ,
,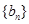 的公比为
的公比为 ,则
,则 为正整数,
为正整数, ,
,
依题意有
 ,即
,即 ,
,解得
 或者
或者 (舍去),
(舍去),故
 。 4分
。 4分(2)
 。 6分
。 6分 ,
, ,
,两式相减得
 8分
8分 ,
,所以
 12分
12分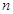 项和.
项和.
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
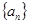 的各项均为正数,且
的各项均为正数,且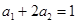 ,
,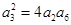 .
.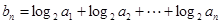 ,求数列
,求数列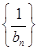 的前
的前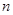 项和.
项和.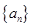 ,
,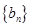 满足
满足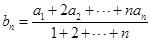
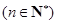 .
.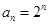 ,求数列
,求数列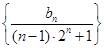 的前
的前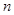 项和
项和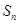 .
.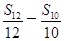 =2,则S2 014的值等于( ).
=2,则S2 014的值等于( ).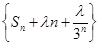 为等差数列?若存在,求出λ的值;若不存在,则说明理由.
为等差数列?若存在,求出λ的值;若不存在,则说明理由. 的公差
的公差 ,
, ,若
,若 是
是 与
与 的等比中项,则
的等比中项,则 =( )
=( ) 的前n项和为Sn,且S3=6,a1=4,则公差d等于 ( )
的前n项和为Sn,且S3=6,a1=4,则公差d等于 ( )