题目内容

已知x1,x2均为正数，求证：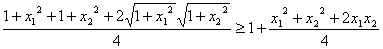

思路分析：待证不等式较为复杂，首先想到化简，由于均为正数，两边平方进而用基本不等式可证之；当然另一方面，用反证法也不失为一个好的选择.

证明：（分析法）由于不等式两边均为正数，平方后只须证：

,

即：≥1+x1x2,

再平方得：（1+x12）(1+x22)≥1+2x1x2+x12x22,

化简整理得：x12+x22≥2x1x2（显然成立）,

∴原式成立.

（反证法）假设,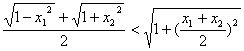

化简可得：x12+x22＜2x1x2（不可能）,

∴原式成立.

练习册系列答案
相关题目
已知函数f（x）=
124
ax3-bx2+（2-b）x+1（x＞0）在x=x1和x=x2处取得极值，且0＜x1＜1＜x2＜2．
（Ⅰ）若a，b均为正整数，求函数f（x）的单调增区间；
（Ⅱ）若z=a-12b，求z的取值范围．
已知 100m=5，10n=2．
（1）求 2m+n的值；
（2）x1、x2、…、x10均为正实数，若函数f（x）=logax（a＞0且a≠1），且f（x1•x2•…•x10）=2m+n，求f（x12）+f（x22）+…+f（x102）的值．

（本小题10分）已知，，

(1)求的值.

(2) x1、x2、…x2010均为正实数，若函数f(x)＝logax(a＞0且a≠1)且f(x1x2…x2010)＝，

求f()＋f()＋…＋f()的值
已知 100m=5，10n=2．
（1）求 2m+n的值；
（2）x1、x2、…、x10均为正实数，若函数f（x）=logax（a＞0且a≠1），且f=2m+n，求f（x12）+f（x22）+…+f（x102）的值．
已知 100m=5，10n=2．
（1）求 2m+n的值；
（2）x1、x2、…、x10均为正实数，若函数f（x）=logax（a＞0且a≠1），且f=2m+n，求f（x12）+f（x22）+…+f（x102）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网