Question

已知函数f（x）=

1

24

ax³-bx²+（2-b）x+1（x＞0）在x=x₁和x=x₂处取得极值，且0＜x₁＜1＜x₂＜2．
（Ⅰ）若a，b均为正整数，求函数f（x）的单调增区间；
（Ⅱ）若z=a-12b，求z的取值范围．

Answer 1

分析：（I）对函数f（x） 求导，利用条件可得x₁，x₂是f′（x）=0的根，结合根的分布可得

f′(0)＞0 f′(1)＜0 f′(2)＞0

求出a，b，分别令f′（x）＞0，f′（x）＜0，解函数的单调区间．
（II）结合（I）可找出a，b所表示的平面区域，利用线性规划的知识，求目标函数Z的取值范围．

解答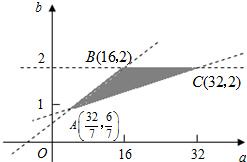：解：由题意得f′(x)=

1

8

ax2-2bx+2-b，（1分）
∵0＜x₁＜1＜x₂＜2，
∴

f′(0)＞0 f′(1)＜0 f′(2)＞0.

即

2-b＞0 1 8 a-2b+2-b＜0 1 2 a-4b+2-b＞0.

整理得

2-b＞0 a-24b+16＜0 a-10b+4＞0

（3分）
（Ⅰ）由a，b均为正整数得a=7，b=1．（5分）
即f′(x)=

7

8

x2-2x+1，令f′(x)=

7

8

x2-2x+1＞0，
解得：x＜

8-2 2

7

，或x＞

8+2 2

7

．
所以函数f（x）的单调增区间为(-∞，

8-2 2

7

)，(

8+2 2

7

，+∞)．（8分）
（Ⅱ）由已知得

2-b＞0 a-24b+16＜0 a-10b+4＞0

此不等式组表示的区域为平面aOb上三条直线：2-b=0，a-24b+16=0，a-10b+4=0所围成的△ABC的内部．（10分）
其三个顶点分别为：A(

32

7

，

6

7

)，B(16，2)，C(32，2)，z在这三点的值依次为-

40

7

，-8，8，
所以z的取值范围为（-8，8）．（12分）
（无图形，扣1分）

点评：本题是一道综合性较好的试题，综合考查了函数的极值、二次方程的实根分布问题，线性规划中求目标函数的取值范围，解决问题的关键是由极值问题转化为关于a，b的二元一次不等式組，确定a，b所表示的平面区域，进而求目标函数Z的取值范围．