题目内容
【题目】用![]() 表示一个小于或等于
表示一个小于或等于![]() 的最大整数.如:
的最大整数.如:![]() ,
,![]() ,
,![]() . 已知实数列
. 已知实数列![]() 、
、![]() 、
、![]() 对于所有非负整数
对于所有非负整数![]() 满足
满足![]() ,其中
,其中![]() 是任意一个非零实数.
是任意一个非零实数.
(Ⅰ)若![]() ,写出
,写出![]() 、
、![]() 、
、![]() ;
;
(Ⅱ)若![]() ,求数列
,求数列![]() 的最小值;
的最小值;
(Ⅲ)证明:存在非负整数![]() ,使得当
,使得当![]() 时,
时,![]() .
.
【答案】(Ⅰ)![]() ,
,![]() ,
,![]() ;(Ⅱ)最小值为
;(Ⅱ)最小值为![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】
(Ⅰ)由![]() ,代入可得
,代入可得![]() ,同理可得:
,同理可得:![]() 、
、![]() ;
;
(Ⅱ)由![]() ,可得
,可得![]() ,
,![]() ,设
,设![]() ,
,![]() ,可得
,可得![]() ,因此
,因此![]() ,
,![]() . 又因
. 又因![]() ,可得
,可得![]() ,
,![]() . 假设
. 假设![]() ,都有
,都有![]() 成立,可得:
成立,可得:![]() ,
,![]() ,利用累加求和方法可得
,利用累加求和方法可得![]() ,
,![]() ,则当
,则当![]() 时,
时,![]() ,得出矛盾,
,得出矛盾,![]() ,从而可得出
,从而可得出![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,由(Ⅱ)知,存在
时,由(Ⅱ)知,存在![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,由此得出
,由此得出![]() ,
,![]() ,成立.;若
,成立.;若![]() ,
,![]() ,推导出数列
,推导出数列![]() 单调不减.由
单调不减.由![]() 是负整数,可知存在整数
是负整数,可知存在整数![]() 和负整数
和负整数![]() ,使得当
,使得当![]() 时,
时,![]() .所以,当
.所以,当![]() 时,
时,![]() ,转化为
,转化为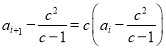 ,令
,令![]() ,即
,即![]() ,
,![]() .经过讨论:当
.经过讨论:当![]() 时,得证.当
时,得证.当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() ,则
,则![]() 有界,进而证明结论.
有界,进而证明结论.
(Ⅰ)![]() ,
,![]() ,
,
同理可得:![]() ,
,![]() ;
;
(Ⅱ)因![]() ,则
,则![]() ,所以
,所以![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() .
.
又因![]() ,则
,则![]() ,则
,则![]() ,
,![]() .
.
假设![]() ,都有
,都有![]() 成立,则
成立,则![]() ,
,
则![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
则![]() ,
,![]() ,则当
,则当![]() 时,
时,![]() ,
,
这与假设矛盾,所以![]() ,
,![]() 不成立,
不成立,
即存在![]() ,
,![]() ,从而
,从而![]() 的最小值为
的最小值为![]() ;
;
(Ⅲ)当![]() 时,由(Ⅱ)知,存在
时,由(Ⅱ)知,存在![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() ,成立.
,成立.
当![]() 时,若存在
时,若存在![]() ,
,![]() ,则
,则![]() ,
,![]() ,得证;
,得证;
若![]() ,
,![]() ,则
,则![]() ,则
,则![]() ,
,
则![]() ,
,![]() ,所以数列
,所以数列![]() 单调不减.
单调不减.
由于![]() 是负整数,所以存在整数m和负整数c,使得当
是负整数,所以存在整数m和负整数c,使得当![]() 时,
时,![]() .
.
所以,当![]() 时,
时,![]() ,则
,则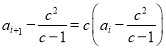 ,令
,令![]() ,
,
即![]() ,
,![]() .
.
当![]() 时,则
时,则![]() ,
,![]() ,则
,则![]() ,
,![]() ,得证.
,得证.
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因当![]() 时,
时,![]() ,则
,则![]() ,则
,则![]() 有界,
有界,
所以![]() ,所以负整数
,所以负整数![]() .
.
![]() ,则
,则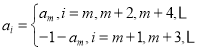
令![]() ,满足当
,满足当![]() 时,
时,![]() .
.
综上,存在非负整数![]() ,使得当
,使得当![]() 时,
时,![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目