Question

【题目】如图， 、分别为直角三角形的直角边和斜边的中点，沿将折起到的位置，连结、， 为的中点．

（1）求证： 平面；（2）求证：平面平面；

（3）求证： 平面．

Answer 1

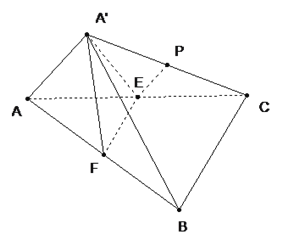
【答案】(1) 证明见解析；(2) 证明见解析；(3) 证明见解析

【解析】试题分析：

（1）欲证EP∥平面，关键在平面内找一直线与平行，由E、P分别为AC、A′C的中点，可得平行与面内一直线；（2）欲证平面垂直平面，根据面面垂直的判定定理可知一平面经过另一平面的垂线则这两个面垂直；（3）欲证⊥平面,即证垂直平面内的两条相交直线，易证.

试题解析：(1)证明： E、P分别为AC、A′C的中点，

EP∥A′A，又A′A平面AA′B，EP平面AA′B

∴即EP∥平面A′FB

(2) 证明：∵BC⊥AC，EF⊥A′E，EF∥BC

∴BC⊥A′E，∴BC⊥平面A′EC

BC平面A′BC

∴平面A′BC⊥平面A′EC

(3)证明：在△A′EC中，P为A′C的中点，∴EP⊥A′C，

在△A′AC中，EP∥A′A，∴A′A⊥A′C

由(2)知：BC⊥平面A′EC 又A′A平面A′EC

∴BC⊥AA′， ∴A′A⊥平面A′BC