题目内容
9.若x0是方程($\frac{1}{2}$)x=x${\;}^{\frac{1}{3}}$的解,则x0属于区间(0,1).分析 由题意设f(x)=($\frac{1}{2}$)x-x${\;}^{\frac{1}{3}}$,将方程的根转化为函数f(x)的零点,再判断出f(x)的单调性,利用函数零点存在性判断定理可得x0属于区间.
解答 解:由题意设f(x)=($\frac{1}{2}$)x-x${\;}^{\frac{1}{3}}$,
则方程($\frac{1}{2}$)x=x${\;}^{\frac{1}{3}}$的解x0是函数f(x)的零点,
∵函数f(x)是定义域上的减函数,且f(0)=1>0、f(1)=$-\frac{1}{2}$<0,
∴函数f(x)的零点x0∈(0,1),
故答案为:(0,1).
点评 本题考查方程的根与对应函数的零点问题,以及函数零点存在性判断定理,属于基础题.

练习册系列答案
相关题目
2.已知函数f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$,x∈R,若对任意θ∈(0,$\frac{π}{2}$],都有f(sinθ)+f(1-m)>0成立,则实数m的取值范围是( )
| A. | (0,1) | B. | (0,2) | C. | (-∞,1) | D. | (-∞,1] |
 (
( ,
, 为常数,
为常数, )满足
)满足 ,且
,且 有唯一解.
有唯一解. 的解析式;
的解析式; ,且
,且 (
( ,
, ),求证:数列
),求证:数列 为等差数列.
为等差数列. 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左准线l的距离为3.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左准线l的距离为3. ,
, ,
, ,
, ,
, ,
, ,…
,… ,1,
,1, ,
, ,…
,…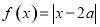 ,
, .
.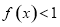 的解集为
的解集为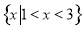 ,求
,求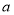 的值;
的值;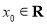 ,使
,使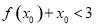 ,求
,求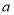 的取值范围.
的取值范围.