题目内容
若直线3x+4y-12=0与圆（x-3）2+（y-2）2=4相交于M，N两点，则线段MN的长为________．
2
分析：求出圆心坐标和圆的半径r，利用点到直线的距离公式求出圆心到已知直线的距离d，由求出的d与半径r，根据垂径定理与勾股定理求出|MN|的一半，即可得到|MN|的长．
解答：圆（x-3）2+（y-2）2=4，
∴圆心坐标为（3，2），半径r=2，
∴圆心到直线3x+4y-12=0的距离d=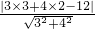
=1，
则|MN|=2
=2
=
．
故答案为：2
点评：此题考查了直线与圆相交的性质，勾股定理以及垂径定理，考查了数形结合的思想．当直线与圆相交时，常常过圆心作直线的垂直，由弦心距、圆的半径以及弦长得一半构造直角三角形，利用勾股定理求出直线被圆所截得弦的长度．
分析：求出圆心坐标和圆的半径r，利用点到直线的距离公式求出圆心到已知直线的距离d，由求出的d与半径r，根据垂径定理与勾股定理求出|MN|的一半，即可得到|MN|的长．
解答：圆（x-3）2+（y-2）2=4，
∴圆心坐标为（3，2），半径r=2，
∴圆心到直线3x+4y-12=0的距离d=
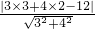=1，则|MN|=2
=2=．故答案为：2
点评：此题考查了直线与圆相交的性质，勾股定理以及垂径定理，考查了数形结合的思想．当直线与圆相交时，常常过圆心作直线的垂直，由弦心距、圆的半径以及弦长得一半构造直角三角形，利用勾股定理求出直线被圆所截得弦的长度．
练习册系列答案
全能测控期末小状元系列答案
相关题目
A．若不等式|x-1|+|x-m|＜2m的解集为∅，则m的取值范围为