��Ŀ����
����Ŀ����ѧ���������ú��ٲμ����ʵ�����Ի�е���۹�˾7�·���11�·�����ij�ֻ�е����������������۵��۽����˵��飬���۵���xԪ��������y��֮���һ�����������ʾ��
�·� | 7 | 8 | 9 | 10 | 11 |
���۵���xԪ | 9 | 9.5 | 10 | 10.5 | 11 |
������y�� | 11 | 10 | 8 | 6 | 5 |
��1������7��11�·ݵ����ݣ����y����x�Ļع�ֱ�߷��̣�
��2��Ԥ���ڽ��������У������������۵�����Ȼ���ӣ�1���еĹ�ϵ�������ֻ�������ijɱ���2.5Ԫ/������ô����������۵���Ӧ��Ϊ����Ԫ���ܻ��������� �ο���ʽ���ع�ֱ�߷��� ![]() =b
=b ![]() +a������b=
+a������b= 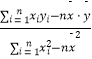 ��
��
�ο����ݣ� ![]() =392��
=392�� ![]() =502.5��
=502.5��
���𰸡�
��1���⣺��Ϊ ![]() =
= ![]() ����9+9.5+10+10.5+11��=10��
����9+9.5+10+10.5+11��=10��
![]() =
= ![]() ����11+10+8+6+5��=8��
����11+10+8+6+5��=8��
���Իع�ϵ��b=  =
= ![]() =��3.2��
=��3.2��
��a= ![]() ��b
��b ![]() =8������3.2����10=40��
=8������3.2����10=40��
����y����x�Ļع�ֱ�߷���Ϊ ![]() =��3.2
=��3.2 ![]() +40��
+40��
��2���⣺����������ΪW����
W=��x��2.5������3.2x+40��=��3.2x2+48x��100�����У�2.5��x��12.5������xû��Χ��1�֣�
��x=7.5ʱ��Wȡ�����ֵΪ80��
���Ըò�Ʒ�����۵��۶�Ϊ7.5Ԫ/��ʱ����õ��������
����������1������ ![]() ��
�� ![]() ������ع�ϵ����д���ع鷽�̣���2�����ݻع鷽�̣�д������������W���������W�����ֵ���ɣ�
������ع�ϵ����д���ع鷽�̣���2�����ݻع鷽�̣�д������������W���������W�����ֵ���ɣ�

