题目内容
20. 如图,在多面体ABCDEF中,平面ADEF⊥平面ABCD,AB∥DC,ADEF是正方形,已知BD=2AD=2,AB=2DC=$\sqrt{5}$.
如图,在多面体ABCDEF中,平面ADEF⊥平面ABCD,AB∥DC,ADEF是正方形,已知BD=2AD=2,AB=2DC=$\sqrt{5}$.(1)证明:平面BDF⊥平面ADEF;
(2)求二面角D-BE-C的正弦值.
分析 (1)由已知得FD⊥平面ABCD,从而BD⊥DE,由勾股定理得AD⊥BD,从而BD⊥平面ADEF,由此能证明平面BDF⊥平面ADEF.
(2)以D为原点,DA为x轴,DB为y轴,DE为z轴,建立空间直角坐标系,求出平面DBC的法向量、平面DBE的法向量,利用向量的夹角公式,即可求二面角D-BE-C的正弦值.
解答 (1)证明:∵平面ADEF⊥平面ABCD,AB∥DC,ADEF是正方形,
∴FD⊥平面ABCD,∴BD⊥DE,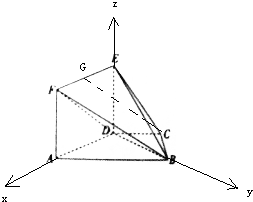
∵BD=2AD=2,AB=2DC=$\sqrt{5}$,
∴由勾股定理得AD⊥BD,
∵AD∩DE=D,∴BD⊥平面ADEF,
∵BD?平面BDF,∴平面BDF⊥平面ADEF.
(2)解:以D为原点,DA为x轴,DB为y轴,DE为z轴,
建立空间直角坐标系,D(0,0,0),E(0,0,1),B(0,2,0),C(-$\frac{1}{2}$,1,0)
$\overrightarrow{BE}$=(0,-2,1),$\overrightarrow{BC}$=(-$\frac{1}{2}$,-1,0),
设平面DBC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{-2y+z=0}\\{-\frac{1}{2}x-y=0}\end{array}\right.$,取x=2,得$\overrightarrow{n}$=(2,-1,-2),
∵平面DBE的法向量为$\overrightarrow{DA}$=(1,0,0)
∴二面角D-BE-C的余弦值为$\frac{2}{\sqrt{4+1+4}•1}$=$\frac{2}{3}$,
∴二面角D-BE-C的正弦值为$\frac{\sqrt{5}}{3}$.
点评 本题考查平面与平面垂直的证明,考查二面角D-BE-C的正弦值的求法,是中档题,解题时要注意向量法的合理运用,确定平面的法向量是关键.

| A. | 1 | B. | 3 | C. | 5 | D. | 9 |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,右焦点F关于直线x-2y=0对称的点在圆x2+y2=4上.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,右焦点F关于直线x-2y=0对称的点在圆x2+y2=4上.
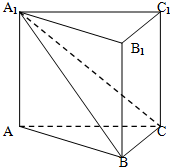 如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.
如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.