题目内容
已知数列{an}的首项为1,对任意的n∈N*,定义bn=an+1-an,
(1)若bn=n+1,求a4;
(2)若bn+1bn-1=bn(n≥2),且b1=a,b2=b(ab≠0),
①当a=1,b=2时,求数列{bn}的前3n项和;
②当a=1时,求证:数列{an}中任意一项的值均不会在该数列中出现无数次。
(1)若bn=n+1,求a4;
(2)若bn+1bn-1=bn(n≥2),且b1=a,b2=b(ab≠0),
①当a=1,b=2时,求数列{bn}的前3n项和;
②当a=1时,求证:数列{an}中任意一项的值均不会在该数列中出现无数次。
解:(1)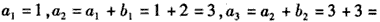 6,
6,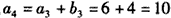 ;
;
(2)①因为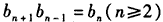 ,
,
所以,对任意的n∈N*有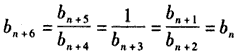 ,
,
即数列{bn}各项的值重复出现,周期为6.
数列{bn}的前6项分别为 ,且这六个数的和为7.
,且这六个数的和为7.
设数列{bn}的前n项和为Sn,
则当n=2k(k∈N*)时, ;
;
当n=2k+1(k∈N*)时,


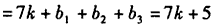 ,
,
所以,当n为偶数时,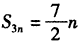 ;当n为奇数时,
;当n为奇数时,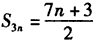 ;
;
②由①知:对任意的n∈N*有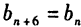 ,
,
又数列{bn}的前6项分别为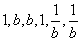 ,且这六个数的和为
,且这六个数的和为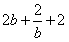 ;
;
设 (其中i为常数且i∈{1,2,3,4,5,6}),
(其中i为常数且i∈{1,2,3,4,5,6}),
所以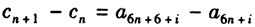

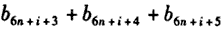
 ,
,
所以,数列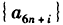 均为以
均为以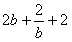 为公差的等差数列,
为公差的等差数列,
因为b>0时, ;b<0 时,
;b<0 时,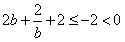 ,
,
所以 是公差不为零的等差数列,其中任何一项的值最多在该数列中出现一次,
是公差不为零的等差数列,其中任何一项的值最多在该数列中出现一次,
所以数列{an}中任意一项的值最多在此数列中出现6次,
即任意一项的值不会在此数列中重复出现无数次.
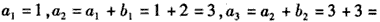 6,
6,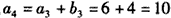 ;
;(2)①因为
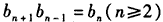 ,
,所以,对任意的n∈N*有
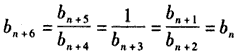 ,
,即数列{bn}各项的值重复出现,周期为6.
数列{bn}的前6项分别为
 ,且这六个数的和为7.
,且这六个数的和为7.设数列{bn}的前n项和为Sn,
则当n=2k(k∈N*)时,
 ;
;当n=2k+1(k∈N*)时,


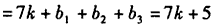 ,
,所以,当n为偶数时,
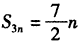 ;当n为奇数时,
;当n为奇数时,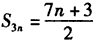 ;
;②由①知:对任意的n∈N*有
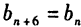 ,
,又数列{bn}的前6项分别为
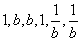 ,且这六个数的和为
,且这六个数的和为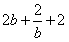 ;
;设
 (其中i为常数且i∈{1,2,3,4,5,6}),
(其中i为常数且i∈{1,2,3,4,5,6}),所以
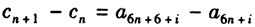

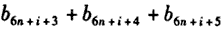
 ,
,所以,数列
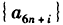 均为以
均为以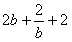 为公差的等差数列,
为公差的等差数列,因为b>0时,
 ;b<0 时,
;b<0 时,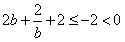 ,
,所以
 是公差不为零的等差数列,其中任何一项的值最多在该数列中出现一次,
是公差不为零的等差数列,其中任何一项的值最多在该数列中出现一次,所以数列{an}中任意一项的值最多在此数列中出现6次,
即任意一项的值不会在此数列中重复出现无数次.

练习册系列答案
相关题目