题目内容
已知函数 .
.
(Ⅰ) 求函数 的最小值和最小正周期;
的最小值和最小正周期;
(Ⅱ)已知 内角
内角 的对边分别为
的对边分别为 ,且
,且 ,若向量
,若向量 与
与 共线,求
共线,求 的值.
的值.
解:(Ⅰ)

 ……………………………………………………3分
……………………………………………………3分
∴  的最小值为
的最小值为 ,最小正周期为
,最小正周期为 . ………………………………5分
. ………………………………5分
(Ⅱ)∵  , 即
, 即
∵  ,
, ,∴
,∴  ,∴
,∴  . ……7分
. ……7分
∵  共线,∴
共线,∴  .
.
由正弦定理  , 得
, 得 ①…………………………………9分
①…………………………………9分
∵  ,由余弦定理,得
,由余弦定理,得 , ②……………………10分
, ②……………………10分
解方程组①②,得 . …………………………………………12分
. …………………………………………12分
解析

练习册系列答案
相关题目
设 且
且 则( )
则( )
A. | B. |
C. | D. |
 是( ).
是( ).
| A.奇函数 |
| B.偶函数 |
| C.既是奇函数也是偶函数 |
| D.既不是奇函数也不是偶函数 |
 的值为 ( )
的值为 ( )
A. | B. | C. | D. |
过平面区域 内一点
内一点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为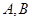 ,记
,记 ,则当
,则当 最小时
最小时 的值为( )
的值为( )
A.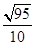 | B. | C. | D. |
 上的函数
上的函数
 的最小正周期为
的最小正周期为 .
. ,
, ,求
,求 ,
, ,求
,求 的值
的值 ,其中
,其中 .
. 满足
满足 ,且
,且 的图象关于直线
的图象关于直线 对称.
对称. 的值;
的值; 的方程
的方程 在区间
在区间 上总有实数解,求实数
上总有实数解,求实数 的取值范围.
的取值范围.
 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。 ,且b=1,c=2,求a的值。
,且b=1,c=2,求a的值。 +φ)>Asin(ω
+φ)>Asin(ω +φ)?若存在,求出m.若不存在,说明理由.
+φ)?若存在,求出m.若不存在,说明理由.