题目内容
16.己知函数f(x)=-x2+|x-a|,a∈R.(1)讨论f(x)的奇偶性,并证明你的结论;
(2)当a=-1时,求f(x)的值域;
(3)当a≤0时,求f(x)的最大值.
分析 (1)当a=0时,f(x)为偶函数;当a≠0时,f(x)为非奇非偶函数;
(2)将a=-1代入,分类讨论f(x)的取值范围,最后综合讨论结果,可得答案;
(3)结合二次函数的图象和性质,分类讨论f(x)的取值范围,最后综合讨论结果,可得答案;
解答 解:(1)当a=0时,f(x)为偶函数;当a≠0时,f(x)为非奇非偶函数,理由如下:
当a=0时,函数f(-x)=-(-x)2+|-x|+1=-x2+|x|=f(x),此时,f(x)为偶函数.
当a≠0时,f(a)=-a2,f(-a)=-a2+2|a|,f(a)≠f(-a),f(a)≠-f(-a),
此时f(x)既不是奇函数,也不是偶函数.
(2)当a=-1时,函数f(x)=-x2+|x+1|,
当x≤-1时,f(x)=-x2-x-1∈(-∞,-1],
当x>-1时,f(x)=-x2+x+1∈(-∞,$\frac{5}{4}$],
综上,当a=-1时,求f(x)的值域为(-∞,$\frac{5}{4}$],
(3)当a≤0时,
当x≤a时,f(x)=-x2-x+a的图象开口朝下,以x=$-\frac{1}{2}$为对称轴,
此时函数f(x)≤$\frac{1}{4}$+a,
当x>a时,f(x)=-x2-x+a的图象开口朝下,以x=$\frac{1}{2}$为对称轴,
f(x)=-x2+x-a∈(-∞,$\frac{1}{4}$-a],
∵$\frac{1}{4}$-a>$\frac{1}{4}$+a,
故当a≤0时,f(x)的最大值为$\frac{1}{4}$-a.
点评 本题考查的知识点是分段函数的应用,二次函数的图象和性质,函数的奇偶性,是函数图象和性质的综合应用,难度中档.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
6.设函数f(x)=$\left\{\begin{array}{l}{4+x,x≤0}\\{{x}^{2},x>0}\end{array}\right.$,若f[f(a)]>f[f(a)+1],则实数a的取值范围为( )
| A. | (-1,0] | B. | [-1,0] | C. | (-5,-4] | D. | [-5,-4] |
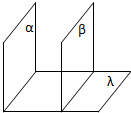 如图,α、β、λ是三个平面,满足α⊥γ,α∥β,求证:β⊥γ.
如图,α、β、λ是三个平面,满足α⊥γ,α∥β,求证:β⊥γ.