题目内容
求证:等轴双曲线x2-y2=a2上任意一点P到两焦点的距离的积等于P到中心距离的平方.
证明:由题意,双曲线的焦点F1、F2的坐标分别为(-
a,0)、(
a,0),
设P点的坐标为(x0,y0),则x02-y02=a2.
于是
,
.
又|PO|2=x02+y02=x02+x02-a2=2x02-a2,
∴|PF1|·|PF2|=|PO|2.
启示:双曲线x2-y2=a2上点P的坐标(x0,y0)应适合关系x02-y02=a2,是本题证明的关键.
练习册系列答案
相关题目
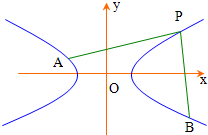（2005•武汉模拟）已知等轴双曲线C：x2-y2=a2 （a＞0）上一定点P（x0，y0）及曲线C上两动点AB满足（
-
）•（
-
）=0，（其中O为原点）
+
）•（
+
）=0；
，1）作两条相互垂直的直线分别交双曲线C于A、B两点.
，求直线PA的斜率.