题目内容
已知双曲线
-
=1（b＞0）的离心率为2，则它的一焦点到其中一条渐近线的距离为 ．
【答案】分析：利用双曲线的离心率，求出b，推出渐近线方程，然后求出它的一焦点到其中一条渐近线的距离．
解答：解：因为双曲线
-
=1（b＞0），所以a=2，双曲线的离心率为2，
所以c=4，所以4+b2=16，b=2
．
双曲线的右焦点坐标（4，0）．
双曲线的一条渐近线方法为：
，即
．
焦点到其中一条渐近线的距离为：
=2
．
故答案为：2
．
点评：本题考查双曲线的基本性质，离心率、渐近线方法的应用，点到直线的距离公式的应用，考查计算能力．
解答：解：因为双曲线
-=1（b＞0），所以a=2，双曲线的离心率为2，所以c=4，所以4+b2=16，b=2
．双曲线的右焦点坐标（4，0）．
双曲线的一条渐近线方法为：
，即．焦点到其中一条渐近线的距离为：
=2．故答案为：2
．点评：本题考查双曲线的基本性质，离心率、渐近线方法的应用，点到直线的距离公式的应用，考查计算能力．
练习册系列答案
相关题目
=1(a,b＞0)的左、右焦点分别为F1、F2,左、右顶点分别为A1、A2,P为双曲线上任意一点,则分别以线段PF1、A1A2为直径的两个圆的位置关系是
-
=1（b＞0）的离心率为2，则它的一焦点到其中一条渐近线的距离为 ．
-
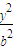=1（b∈N*） 的两个焦点为F1、F2，P是双曲线上的一点，且满足|PF1|-|PF2|=|F1F2|2，|PF2|＜4，
-
=1（b∈N*） 的两个焦点为F1、F2，P是双曲线上的一点，且满足|PF1|-|PF2|=|F1F2|2，|PF2|＜4，