题目内容
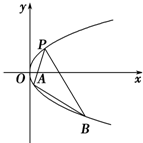 如图所示,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.当PA与PB的斜率存在且倾斜角互补时,直线AB的斜率为定值.这个定值为
如图所示,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.当PA与PB的斜率存在且倾斜角互补时,直线AB的斜率为定值.这个定值为-1
-1
.分析:设直线PA的斜率为kPA,直线PB的斜率为kPB,则可分别表示kPA和kPB,根据倾斜角互补可知kPA=-kPB,进而求得y1+y2的值,把A,B代入抛物线方程两式相减后即可求得直线AB的斜率.
解答:解:设直线PA的斜率为kPA,直线PB的斜率为kPB,
则kPA=
(x1≠1),kPB=
(x2≠1),
∵PA与PB的斜率存在且倾斜角互补,
∴kPA=-kPB,
由A(x1,y1),B(x2,y2)在抛物线上,得y12=4x1(1)
y22=4x2(2),
∴
=-
,
∴y1+2=-(y2+2)
∴y1+y2=-4
由(1)-(2)得直线AB的斜率
=
=-1.
故答案为:-1.
则kPA=
| y1-2 |
| x1-1 |
| y2-2 |
| x2-1 |
∵PA与PB的斜率存在且倾斜角互补,
∴kPA=-kPB,
由A(x1,y1),B(x2,y2)在抛物线上,得y12=4x1(1)
y22=4x2(2),
∴
| y1-2 | ||
|
| y2-2 | ||
|
∴y1+2=-(y2+2)
∴y1+y2=-4
由(1)-(2)得直线AB的斜率
| y2-y1 |
| x2-x1 |
| 4 |
| y1+y2 |
故答案为:-1.
点评:本小题主要考查直线、抛物线等基本知识,考查运用解析几何的方法分析问题和解决问题的能力,属于中档题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km其中曲线段AF是以A为顶点、AD为对称轴的抛物线的一部分.分别以直线AB,AD为x轴和y轴建立平面直角坐标系.
某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km其中曲线段AF是以A为顶点、AD为对称轴的抛物线的一部分.分别以直线AB,AD为x轴和y轴建立平面直角坐标系. 如图所示,已知二次函数y=-x2+9,矩形ABOC的顶点A在第一象限内,且A在抛物线上,顶点B、C分别在y轴、x轴上,设点A的坐标为(x,y).
如图所示,已知二次函数y=-x2+9,矩形ABOC的顶点A在第一象限内,且A在抛物线上,顶点B、C分别在y轴、x轴上,设点A的坐标为(x,y). (2012•大丰市一模)如图所示,已知平面直角坐标系xOy,抛物线y=-x2+bx+c过点A(4,0)、B(1,3).
(2012•大丰市一模)如图所示,已知平面直角坐标系xOy,抛物线y=-x2+bx+c过点A(4,0)、B(1,3). 和抛物线
和抛物线 有公共焦点
有公共焦点 ,
,  的直线
的直线 与抛物线
与抛物线 两点
两点 ,求直线
,求直线 关于直线
关于直线 在抛物线
在抛物线