题目内容
若函数 的零点都在(-∞,-2]∪[2,+∞)内,则
的零点都在(-∞,-2]∪[2,+∞)内,则 的最小值为________.
的最小值为________.
16
分析:根据均值不等式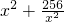 ≥2
≥2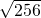 =32,从而求出a+b的范围,利用线性规划的问题,可知
=32,从而求出a+b的范围,利用线性规划的问题,可知 表示原点到可行域的距离,从而求解;
表示原点到可行域的距离,从而求解;
解答: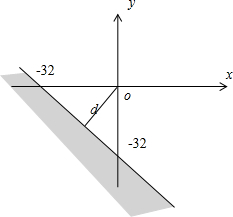 解:函数
解:函数 的零点都在(-∞,-2]∪[2,+∞)内,
的零点都在(-∞,-2]∪[2,+∞)内,
∵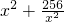 ≥2
≥2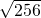 =32,(x=±4等号成立),
=32,(x=±4等号成立),
∴a+b≤-32,可以令x=a,y=b,
画出可行域:
 =
= 表示原点到可行域的距离,如图最小值即为原点到直线的距离d,
表示原点到可行域的距离,如图最小值即为原点到直线的距离d,
∴d=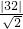 =16
=16 ,
,
∴ ≥16
≥16 ,
,
故答案为16 ;
;
点评:本题考查等价转化的能力、数学结合的数学方法、利用线性规划求函数的最值,是一道好题;

分析:根据均值不等式
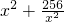 ≥2
≥2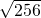 =32,从而求出a+b的范围,利用线性规划的问题,可知
=32,从而求出a+b的范围,利用线性规划的问题,可知 表示原点到可行域的距离,从而求解;
表示原点到可行域的距离,从而求解;解答:
 解:函数
解:函数 的零点都在(-∞,-2]∪[2,+∞)内,
的零点都在(-∞,-2]∪[2,+∞)内,∵
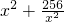 ≥2
≥2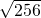 =32,(x=±4等号成立),
=32,(x=±4等号成立),∴a+b≤-32,可以令x=a,y=b,
画出可行域:
 =
= 表示原点到可行域的距离,如图最小值即为原点到直线的距离d,
表示原点到可行域的距离,如图最小值即为原点到直线的距离d,∴d=
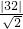 =16
=16 ,
,∴
 ≥16
≥16 ,
,故答案为16
 ;
;点评:本题考查等价转化的能力、数学结合的数学方法、利用线性规划求函数的最值,是一道好题;

练习册系列答案
相关题目