题目内容
【题目】已知数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() .
.
①设![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
②若数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,求实数
,求实数![]() 的最小值;
的最小值;
(2)若数列![]() 的奇数项与偶数项分别成等差数列,且
的奇数项与偶数项分别成等差数列,且![]() ,
,![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
【答案】(1)①见解析②![]() 的最小值为6.(2)
的最小值为6.(2)![]() ,
,![]() .
.
【解析】
(1)①由已知![]() 可得
可得 ,又
,又![]() ,再利用等比数列的定义即可;②利用累计法可得
,再利用等比数列的定义即可;②利用累计法可得![]() 是以6为首项,
是以6为首项,![]() 为公比的等比数列,再用公式法求得
为公比的等比数列,再用公式法求得![]() 即可;
即可;
(2)设奇数项所成等差数列的公差为![]() ,偶数项所成等差数列的公差为
,偶数项所成等差数列的公差为![]() ,对n分n为奇数和偶数进行讨论,结合
,对n分n为奇数和偶数进行讨论,结合![]() ,
,![]() 可得
可得![]() ,进一步得到数列
,进一步得到数列![]() 的通项公式.
的通项公式.
(1)①因为 ,且
,且![]() ,
,
所以数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
②由①知,![]() ,
,
所以![]()

 ,
,
则 ,所以
,所以![]() 是以6为首项,
是以6为首项,![]() 为公比的等比数列,
为公比的等比数列,
所以 .
.
当![]() 时,
时,![]() 有最大值6,所以实数
有最大值6,所以实数![]() 的最小值为6.
的最小值为6.
(2)设奇数项所成等差数列的公差为![]() ,偶数项所成等差数列的公差为
,偶数项所成等差数列的公差为![]()
①当![]() 为奇数时,
为奇数时,![]() ,
,![]() ,
,
则![]() ,即
,即![]() ,
,
所以 ,故
,故![]() .
.
②当![]() 为偶数时,
为偶数时,![]() ,
,![]() ,
,
则![]() ,即
,即![]() ,
,
所以 ,故
,故 .
.
综上可得,![]() .
.
又![]() ,所以
,所以![]() .
.
所以当![]() 为奇数时,
为奇数时,![]() ;
;
当![]() 为偶数时,
为偶数时,![]() .
.
故数列![]() 的通项公式为
的通项公式为![]() ,
,![]() .
.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案【题目】近年来,“无桩有站”模式的公共自行车日益普及,即传统自行车加装智能锁,实现扫码租车及刷卡租车、某公司量产了甲、乙两种款式的公共自行车并投人使用,为了调查消费者对两种自行车的租赁情况,现随机抽取这两种款式的自行车各100辆,分别统计了每辆车在某周内的出租次数,得到甲、乙两种自行车这周内出租次数的频数分布表:
甲 | |||||
出租次数(单位:次) |
|
|
|
|
|
频数 | 10 | 10 | 60 | 15 | 5 |
乙 | |||||
出租次数(单位:次) |
|
|
|
|
|
频数 | 20 | 25 | 25 | 10 | 20 |
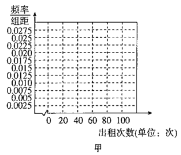
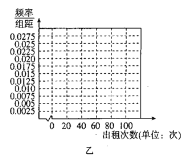
(1)根据频数分布表,完成上面频率分布直方图,并根据频率分布直方图比较甲、乙两种自行车这周内出租次数方差的大小(不必说明理由);
(2)如果两种自行车每次出租获得的利润相同,该公司决定大批量生产其中一种投入某城市使用,请你根据所学的统计知识,给出建议应该生产哪一种自行车,并说明你的理由.