题目内容
直角坐标系xoy中,以原点为极点,x轴的正半轴为极轴建极坐标系,设点A,B分别在曲线C1:
(θ为参数)和曲线C2:ρ=1上,则|AB|的最小值为( )
|
分析:根据题目给出的参数方程和极坐标方程,求出两圆的普通方程,数形结合直观看出曲线上两点的最短距离为两圆的圆心距减去两圆的半径.
解答:解:由
⇒
①2+②2,得C1:(x-3)2+y2=1 ③
又由ρ=1,得C2:x2+y2=1 ④
因为A、B两点分别在两圆上,所以A、B两点的最短距离为两圆的圆心距减去两元的半径,
所以|AB|=
-1-1=1.
故选A.
|
|
①2+②2,得C1:(x-3)2+y2=1 ③
又由ρ=1,得C2:x2+y2=1 ④
因为A、B两点分别在两圆上,所以A、B两点的最短距离为两圆的圆心距减去两元的半径,
所以|AB|=
| (3-0)2+(0-0)2 |
故选A.
点评:本题考查了参数方程化成普通方程和简单曲线的极坐标方程,考查了数形结合思想,解答此题的关键是能正确化出两曲线的普通方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在平面直角坐标系xOy中,不等式组
表示图形的面积等于( )
|
| A、1 | B、2 | C、3 | D、4 |
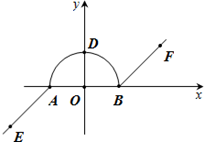 如图,在平面直角坐标系xOy中,我把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段).已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.
如图,在平面直角坐标系xOy中,我把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段).已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.