题目内容
【题目】已知函数![]() ,
,![]() 为
为![]() 的导函数.
的导函数.
(1)证明:![]() 在定义域上存在唯一的极大值点;
在定义域上存在唯一的极大值点;
(2)若存在![]() ,使
,使![]() ,证明:
,证明:![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】
(1)对函数求导得![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上递减,又因为
上递减,又因为![]() ,
,![]() ,判断出单调性,即可证明
,判断出单调性,即可证明![]() 在定义域上存在唯一的极大值点.
在定义域上存在唯一的极大值点.
(2)假设存在![]() ,使
,使![]() ,代入函数得
,代入函数得![]() ,整理得
,整理得![]() .设新函数
.设新函数![]() ,求导结果大于
,求导结果大于![]() ,
,![]() 在
在![]() 上递增,再设
上递增,再设![]() ,则
,则![]() ,即
,即![]() ,
,![]() ,整理可得
,整理可得![]() ,根据对数均值不等式得出
,根据对数均值不等式得出![]() .
.
(1)![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
“![]() ”不能同时取到,所以
”不能同时取到,所以![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上递减,
上递减,
因为![]() ,
,![]() ,
,
所以在定义域![]() 存在唯一
存在唯一![]() ,使
,使![]() 且
且![]() ;
;
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 是
是![]() 在定义域
在定义域![]() 上的唯一极值点且是极大值点.
上的唯一极值点且是极大值点.
(2)存在![]() ,使
,使![]() ,即
,即![]() ,
,
得![]() .
.
设![]() ,则
,则![]() ,
,![]() 在
在![]() 上递增,
上递增,
不妨设![]() ,则
,则![]() ,即
,即![]() ,
,![]() ,
,
所以![]()
![]() ,得
,得![]() ,
,
根据对数均值不等式![]() ,可得
,可得![]() ,
,![]() .
.

练习册系列答案
相关题目
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)求购买金额不少于45元的频率;
(2)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
女 | 18 | ||
合计 |
附:参考公式和数据: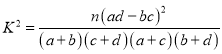 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |