题目内容
已知函数![]()
(1)求![]() 的单调区间;
的单调区间;
(2)对任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
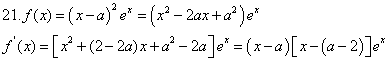
当x变化时,f¢(x)、f(x)的变化如下:
| x | (-∞,a-2) | a-2 | (a-2,a) | a | (a,+∞) |
| f¢(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以f(x)的单调递增区间是(-∞,a-2),(a,+∞),
单调递减区间是(a-2,a). ………7分
(Ⅱ)由(Ⅰ)得[f(x)]极大=f(a-2)=4ea-2.
(1)当a≤1时,f(x)在(-∞,1]上的最大值为f(a-2)或f(1)
由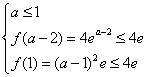 ,解得-1≤a≤1;
,解得-1≤a≤1;
(2)当a-2≤1<a,即1<a≤3时,f(x)在(-∞,1]上的最大值为f(a-2),
此时f (a-2)=4ea-2≤4e3-2=4e;
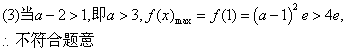
综上,得![]() 取值范围
取值范围![]() ………14分
………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的最小正周期及
的最小正周期及 上的图象.
上的图象. ,
,
 的单调区间;
的单调区间;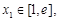 ,都存在
,都存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。 知函数
知函数
 的定义域;
的定义域; 上是减函数.
上是减函数. .
. 的最小正周期;
的最小正周期; 上的最大值和最小值以及取得最大值、最小值时x的值.
上的最大值和最小值以及取得最大值、最小值时x的值.