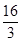题目内容
已知函数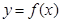 的图像(如图所示)过点
的图像(如图所示)过点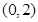 、
、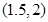 和点
和点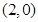 ,且函数图像关于点
,且函数图像关于点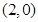 对称;直线
对称;直线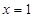 和
和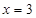 及
及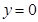 是它的渐近线.现要求根据给出的函数图像研究函数
是它的渐近线.现要求根据给出的函数图像研究函数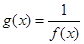 的相关性质与图像,
的相关性质与图像,
(1)写出函数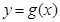 的定义域、值域及单调递增区间;
的定义域、值域及单调递增区间;
(2)作函数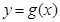 的大致图像(要充分反映由图像及条件给出的信息);
的大致图像(要充分反映由图像及条件给出的信息);
(3)试写出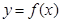 的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分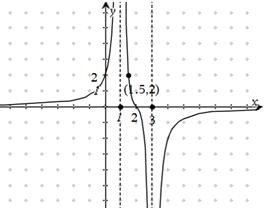
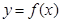 的图像(如图所示)过点
的图像(如图所示)过点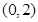 、
、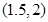 和点
和点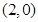 ,且函数图像关于点
,且函数图像关于点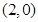 对称;直线
对称;直线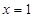 和
和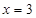 及
及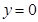 是它的渐近线.现要求根据给出的函数图像研究函数
是它的渐近线.现要求根据给出的函数图像研究函数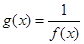 的相关性质与图像,
的相关性质与图像,(1)写出函数
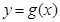 的定义域、值域及单调递增区间;
的定义域、值域及单调递增区间;(2)作函数
 的大致图像(要充分反映由图像及条件给出的信息);
的大致图像(要充分反映由图像及条件给出的信息);(3)试写出
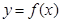 的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
解: (1) 定义域为: 2分
2分
值域为: 3分
3分
函数的单调递增区间为: 和
和 5分
5分
(2)

图像要求能反映出零点( 和
和 ,渐近线
,渐近线 ,过定点,单调性正确. 5分
,过定点,单调性正确. 5分
(3) 结论可能各异如: ,
,

 ,等
,等
层次一:函数图像能满足题意, 但没有说明理由 4分
层次二: 函数图像能满足题意,能简述理由(渐近线、定点等部分内容) 6分
层次三: 函数图像能满足题意,能说明过定点、渐近线、单调性及对称性 9分
 2分
2分值域为:
 3分
3分函数的单调递增区间为:
 和
和 5分
5分(2)

图像要求能反映出零点(
 和
和 ,渐近线
,渐近线 ,过定点,单调性正确. 5分
,过定点,单调性正确. 5分(3) 结论可能各异如:
 ,
, 
 ,等
,等层次一:函数图像能满足题意, 但没有说明理由 4分
层次二: 函数图像能满足题意,能简述理由(渐近线、定点等部分内容) 6分
层次三: 函数图像能满足题意,能说明过定点、渐近线、单调性及对称性 9分
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
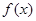 的单调减区间;
的单调减区间;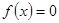 有三个不同的实根,求
有三个不同的实根,求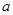 的取值范围;
的取值范围; 在
在 处的切线平行于直线
处的切线平行于直线 ,则
,则


 与直线x+y=2所围图形的面积为______
与直线x+y=2所围图形的面积为______ 之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校. 已知船速为
之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校. 已知船速为 ,车速为
,车速为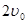 (水流速度忽略不计).
(水流速度忽略不计).
 ,求该学生早晨上学时,从家出发到达学校所用的最短时间.
,求该学生早晨上学时,从家出发到达学校所用的最短时间. ,有
,有 ,
, ,且
,且 时,
时, ,
, ,则
,则 时( )
时( )
 ,
, ,其中
,其中 ,b∈R且b≠0。
,b∈R且b≠0。 的单调区间;
的单调区间; 没有实根,求a的取值范围;
没有实根,求a的取值范围; ,其中
,其中 .
. 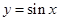 在
在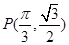 处的切线斜率是 .
处的切线斜率是 .
 ,则a的值是( )
,则a的值是( )