题目内容
本题有2小题,第1小题6分,第2小题10分.
|
 到定直线
到定直线 的距离
的距离 ,
, 为该平面上的动点,过
为该平面上的动点,过 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,且
,且 .
.
(1)试建立适当的平面直角坐标系,求动点 的轨迹
的轨迹 的方程;
的方程;
(2)过点 的直线交轨迹
的直线交轨迹 于
于 、
、 两点,交直线
两点,交直线 于点
于点 ,
,
已知 ,
, ,求证:
,求证: 为定值.
为定值.
【答案】
以线段 所在的直线为
所在的直线为 轴建立直角坐标系
轴建立直角坐标系 .
.
(1)方法一:如图,以线段 的中点为原点
的中点为原点 ,
,
|
 所在的直线为
所在的直线为 轴建立直角坐标系
轴建立直角坐标系 .
.
则, . ……………………………2分
. ……………………………2分
设动点 的坐标为
的坐标为 ,则动点
,则动点 的坐标为
的坐标为
 ,
, , …………2分
, …………2分
由 ,得
,得 ,…2分
,…2分
方法二:由 得,
得, .…………………………2分
.…………………………2分
所以,动点 的轨迹
的轨迹 是抛物线,以线段
是抛物线,以线段 的中点
的中点
为原点 ,以线段
,以线段 所在的直线为
所在的直线为 轴建立直角坐标系
轴建立直角坐标系 ,可得轨迹
,可得轨迹 的方程为:
的方程为: .…………………………………………………………4分
.…………………………………………………………4分
(2)方法一:如图,设直线 的方程为
的方程为 ,
, ,
, ,……1分
,……1分
则 .
……………………………………………………………………………1分
.
……………………………………………………………………………1分
联立方程组 消去
消去 得,
得,
 ,
, ,故 …………………………………………1分
,故 …………………………………………1分
 ……………………………………………………………………………1分
……………………………………………………………………………1分
由 ,
, 得,
得,
 ,
, ,……………………………………………………2分
,……………………………………………………2分
整理得, ,
, ,
,
 .…………………4分
.…………………4分
方法二:由已知 ,
, ,得
,得 . …………………2分
. …………………2分
于是, , ① …………………………………………………3分
, ① …………………………………………………3分
如图,过 、
、 两点分别作准线
两点分别作准线 的垂线,垂足分别为
的垂线,垂足分别为 、
、 ,
,
则有 ② …………………………………………………3分
② …………………………………………………3分
由①,②得 .…………………………………………………………………2分
.…………………………………………………………………2分

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目


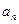 }和{
}和{ }满足:对于任何
}满足:对于任何 ,有
,有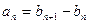 ,
, 为非零常数),且
为非零常数),且 .
. 是
是 与
与 的等差中项,试求
的等差中项,试求 的值,并研究:对任意的
的值,并研究:对任意的 }和{
}和{ }满足:对于任何
}满足:对于任何 ,有
,有 ,
, 为非零常数),且
为非零常数),且 .
. 是
是 与
与 的等差中项,试求
的等差中项,试求 的值,并研究:对任意的
的值,并研究:对任意的 中,
中, ,
, ,
, ,
, .将
.将 所在的直线旋转一周,形成一个几何体.
所在的直线旋转一周,形成一个几何体. ;
;
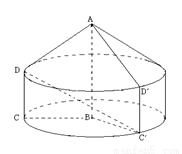 (2)设直角梯形
(2)设直角梯形 (
( )至
)至 ,问:是否存在
,问:是否存在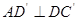 .若存在,求角
.若存在,求角