题目内容
【题目】设数列{an}为等比数列，数列{bn}满足bn=na1+（n﹣1）a2+…+2an﹣1+an ， n∈N* ， 已知b1=m， 
，其中m≠0．
（1）求数列{an}的首项和公比；
（2）当m=1时，求bn；
（3）设Sn为数列{an}的前n项和，若对于任意的正整数n，都有Sn∈[1，3]，求实数m的取值范围．
【答案】
（1）解：由已知b1=a1，
所以a1=m
b2=2a1+a2，
所以 
，
解得 
，
所以数列{an}的公比 
．
（2）解：当m=1时， 
，
bn=na1+（n﹣1）a2++2an﹣1+an①，
②，
②﹣①得
所以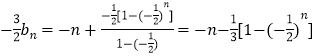 
，
（3）解：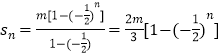 
因为 
，
所以，由Sn∈[1，3]得
，
注意到，当n为奇数时 
，
当n为偶数时 ，
所以 
最大值为 
，最小值为 
．
对于任意的正整数n都有 ，
所以 
，2≤m≤3．
即所求实数m的取值范围是{m|2≤m≤3}．
【解析】（1）由已知中数列{an}为等比数列，我们只要根据bn=na1+（n﹣1）a2+…+2an﹣1+an ， n∈N* ， 已知b1=m， 
，求出a1 ， a2然后根据公比的定义，即可求出数列{an}的首项和公比．（2）当m=1时，结合（1）的结论，我们不难给出数列{an}的通项公式，并由bn=na1+（n﹣1）a2+…+2an﹣1+an ， n∈N*给出bn的表达式，利用错位相消法，我们可以对其进行化简，并求出bn；（3）由Sn为数列{an}的前n项和，及（1）的结论，我们可以给出Sn的表达式，再由Sn∈[1，3]，我们可以构造一个关于m的不等式，解不等式，即可得到实数m的取值范围．在解答过程中要注意对n的分类讨论．
【考点精析】本题主要考查了等比数列的定义和数列的前n项和的相关知识点，需要掌握如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫做等比数列；数列{an}的前n项和sn与通项an的关系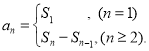
才能正确解答此题．
