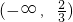题目内容
直线bx-ay+c=0(a>0)是曲线y=ln
在x=3处的切线,f(x)=a•2x+b•3x,若f(x+1)>f(x),则x的取值范围是( )
| 1 |
| x |
分析:先利用导数求出在x=3处切线的斜率,从而得到a与b的等量关系,然后解指数不等式即可求出x的取值范围.
解答:解:y=ln
=-lnx,y′=-
则在x=3处的切线的斜率为y′|x=3=-
=
即b=-
a
∴f(x)=a•2x-
a•3x,
∵f(x+1)>f(x),
∴a•2x+1-
a•3x+1>a•2x-
a•3x,
即2x-
•3x>0即2x-1>3x-1;
即(
)x-1<1=(
)0
∴x-1<0即x<1
故选A.
| 1 |
| x |
| 1 |
| x |
则在x=3处的切线的斜率为y′|x=3=-
| 1 |
| 3 |
| b |
| a |
| 1 |
| 3 |
∴f(x)=a•2x-
| 1 |
| 3 |
∵f(x+1)>f(x),
∴a•2x+1-
| 1 |
| 3 |
| 1 |
| 3 |
即2x-
| 2 |
| 3 |
即(
| 3 |
| 2 |
| 3 |
| 2 |
∴x-1<0即x<1
故选A.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及指数运算,同时考查了运算求解的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在x=3处的切线,f(x)=a•2x+b•3x,若f(x+1)>f(x),则x的取值范围是
在x=3处的切线,f(x)=a•2x+b•3x,若f(x+1)>f(x),则x的取值范围是