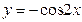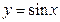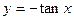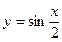题目内容
设a=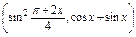 ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b.
(1)求函数f(x)的解析式;
(2)已知常数 >0,若y=f(
>0,若y=f( x)在区间
x)在区间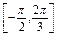 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;
(3)设集合A=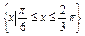 ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A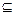 B,求实数m的取值范围.
B,求实数m的取值范围.
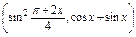 ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b.(1)求函数f(x)的解析式;
(2)已知常数
 >0,若y=f(
>0,若y=f( x)在区间
x)在区间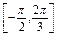 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;(3)设集合A=
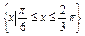 ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A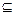 B,求实数m的取值范围.
B,求实数m的取值范围.(1)f(x)=2sinx+1(2) ∈
∈ (3)m∈(1,4)
(3)m∈(1,4)
 ∈
∈ (3)m∈(1,4)
(3)m∈(1,4)(1)f(x)=sin2 ·4sinx+(cosx+sinx)·(cosx-sinx)
·4sinx+(cosx+sinx)·(cosx-sinx)
=4sinx· +cos2x
+cos2x
=2sinx(1+sinx)+1-2sin2x=2sinx+1,
∴f(x)=2sinx+1.
(2)∵f( x)=2sin
x)=2sin x+1,
x+1, >0.
>0.
由2k -
- ≤
≤ x≤2k
x≤2k +
+ ,
,
得f( x)的增区间是
x)的增区间是 ,k∈Z.
,k∈Z.
∵f( x)在
x)在 上是增函数,
上是增函数,
∴
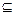
 .
.
∴- ≥
≥ 且
且 ≤
≤ ,∴
,∴ ∈
∈ .
.
(3)由|f(x)-m|<2,得-2<f(x)-m<2,即f(x)-2<m<f(x)+2.
∵A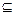 B,∴当
B,∴当 ≤x≤
≤x≤ 时,不等式f(x)-2<m<f(x)+2恒成立.
时,不等式f(x)-2<m<f(x)+2恒成立.
∴f(x)max-2<m<f(x)min+2,
∵f(x)max=f( )=3,f(x)min=f(
)=3,f(x)min=f( )=2,∴m∈(1,4).
)=2,∴m∈(1,4).
 ·4sinx+(cosx+sinx)·(cosx-sinx)
·4sinx+(cosx+sinx)·(cosx-sinx)=4sinx·
 +cos2x
+cos2x=2sinx(1+sinx)+1-2sin2x=2sinx+1,
∴f(x)=2sinx+1.
(2)∵f(
 x)=2sin
x)=2sin x+1,
x+1, >0.
>0.由2k
 -
- ≤
≤ x≤2k
x≤2k +
+ ,
,得f(
 x)的增区间是
x)的增区间是 ,k∈Z.
,k∈Z.∵f(
 x)在
x)在 上是增函数,
上是增函数,∴

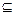
 .
.∴-
 ≥
≥ 且
且 ≤
≤ ,∴
,∴ ∈
∈ .
.(3)由|f(x)-m|<2,得-2<f(x)-m<2,即f(x)-2<m<f(x)+2.
∵A
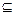 B,∴当
B,∴当 ≤x≤
≤x≤ 时,不等式f(x)-2<m<f(x)+2恒成立.
时,不等式f(x)-2<m<f(x)+2恒成立.∴f(x)max-2<m<f(x)min+2,
∵f(x)max=f(
 )=3,f(x)min=f(
)=3,f(x)min=f( )=2,∴m∈(1,4).
)=2,∴m∈(1,4).
练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 (其中
(其中 ), 那么这一天6时至14时温差的最大值是________
), 那么这一天6时至14时温差的最大值是________ ;与图中曲线对应的函数解析式是________________.
;与图中曲线对应的函数解析式是________________.
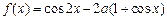 的最小值为
的最小值为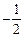 ,则
,则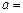 .
. 为 ( )
为 ( )


 的图象与
的图象与 轴交于点
轴交于点 ,且在该点处切线的斜率为
,且在该点处切线的斜率为
 (1)求
(1)求 和
和 的值;(2)已知点
的值;(2)已知点 ,点
,点 是该函数图象上一点,点
是该函数图象上一点,点 是
是 的中点,当
的中点,当 ,
, 时,求
时,求 的值
的值
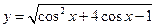 的最大值和最小值.
的最大值和最小值. 在区间
在区间 上的最小值是
上的最小值是 ,则
,则 的取值范围为( )
的取值范围为( )



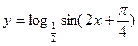 的单调减区间为 ( )
的单调减区间为 ( )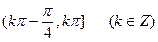
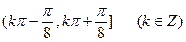
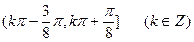
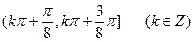
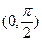 上为增函数且以
上为增函数且以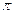 为周期的函数是( ).
为周期的函数是( ).