题目内容
17.已知直线l的参数方程为$\left\{\begin{array}{l}x=1+\frac{t}{2}\\ y=2+\frac{{\sqrt{3}}}{2}t\end{array}\right.$(t为参数),则其直角坐标方程为( )| A. | $\sqrt{3}$x+y+2-$\sqrt{3}$=0 | B. | $\sqrt{3}$x-y+2-$\sqrt{3}$=0 | C. | x-$\sqrt{3}$y+2-$\sqrt{3}$=0 | D. | x+$\sqrt{3}$y+2-$\sqrt{3}$=0 |
分析 消去参数,把直线l的参数方程化为普通方程.
解答 解:因为直线l的参数方程为$\left\{\begin{array}{l}x=1+\frac{t}{2}\\ y=2+\frac{{\sqrt{3}}}{2}t\end{array}\right.$(t为参数),
消去参数t,得直线l的直角坐标方程为y-2=$\sqrt{3}$(x-1),
即$\sqrt{3}$x-y+2-$\sqrt{3}$=0.
故选:B.
点评 本题考查了直线的参数方程化为普通方程的应用问题,是简单题目.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
12.如果cos(π-A)=-$\frac{1}{2}$,那么cosA的值为( )
| A. | --$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
9.设集合A={x|x≤1},B={x|x>p},要使A∩B=∅,则p应满足的条件是( )
| A. | p<1 | B. | p≤1 | C. | p>1 | D. | p≥1 |
6.函数$y=tan\frac{x}{a}$的最小正周期是( )
| A. | aπ | B. | |a|π | C. | $\frac{π}{a}$ | D. | $\frac{π}{|a|}$ |
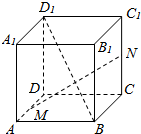 如图所示,在正方体ABCD一A1B1C1D1中,取$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$作为基底.
如图所示,在正方体ABCD一A1B1C1D1中,取$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$作为基底.