题目内容
二次函数f(x)满足:f(1-x)=f(x)且f(0)=1,f(2)=3(1)求f(x)的解析式;
(2)若g(x)=2x+1,求f[g(2)].
【答案】分析:(1)设f(x)=ax2+bx+c,a≠0,由f(1-x)=f(x),f(0)=1,f(2)=3,知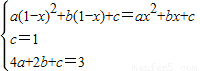 ,由此能求出f(x).
,由此能求出f(x).
(2)由g(x)=2x+1,知g(2)=5,由此能求出f[g(2)].
解答:解:(1)设f(x)=ax2+bx+c,a≠0,
∵f(1-x)=f(x),f(0)=1,f(2)=3,
∴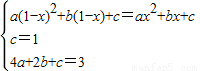 ,
,
即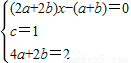 ,
,
由(2a+2b)x-(a+b)=0恒成立,
得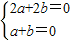 ,即a=-b,又4a+2b=2
,即a=-b,又4a+2b=2
解得a=1,b=-1,c=1,
∴f(x)=x2-x+1.
(2)∵g(x)=2x+1,
∴g(2)=2×2+1=5,
∴f[g(2)]=f(5)=25-5+1=21.
点评:本题考查二次函数的性质和应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
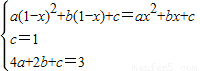 ,由此能求出f(x).
,由此能求出f(x).(2)由g(x)=2x+1,知g(2)=5,由此能求出f[g(2)].
解答:解:(1)设f(x)=ax2+bx+c,a≠0,
∵f(1-x)=f(x),f(0)=1,f(2)=3,
∴
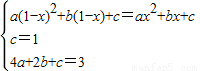 ,
,即
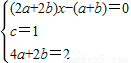 ,
,由(2a+2b)x-(a+b)=0恒成立,
得
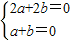 ,即a=-b,又4a+2b=2
,即a=-b,又4a+2b=2解得a=1,b=-1,c=1,
∴f(x)=x2-x+1.
(2)∵g(x)=2x+1,
∴g(2)=2×2+1=5,
∴f[g(2)]=f(5)=25-5+1=21.
点评:本题考查二次函数的性质和应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目