题目内容
已知F1,F2为双曲线C: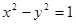 的左右焦点,点P在C上,
的左右焦点,点P在C上,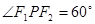 ,则
,则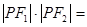 ( )
( )
A . 2 B . 4 C. 6 D. 8
【答案】
B
【解析】
试题分析:在 中,
中, ,
, ,
, …………①
…………①
由余弦定理得:
 ,即
,即

 …………………②
…………………②
把①代入②得: 4.
4.
考点:本题考查双曲线的简单性质,余弦定理。
点评:圆锥曲线上一点与其两焦点所构成的三角形叫做圆锥曲线的焦点三角形。焦点三角形在我们做题时经常见到。当见到焦点三角形的时候一般要联系余弦定理、圆锥曲线的定义来解决。

练习册系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )